A 2004. februári C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C.750.Egy vonat a menetrend szerint indul ki az állomásról. 8 kilométer megtétele után a mozdonyvezető az órájára néz és látja, hogy az óra- és a percmutató pontosan fedi egymást. Az első 8 kilométeren a vonat 33 kilométeres óránkénti átlagsebességgel haladt. Mikor indult el a vonat az állomásról?

Megoldás: A vonat az első 8 kilométert 8/33 óra, vagyis 160/11 perc alatt tette meg. Az órán a mutatók 12/11 óránként, azaz 1 óra 60/11 percenként fedik egymást. Ha a vonat k óra m perckor indult, akkor

k óra m perc + 160/11 perc = l(1 óra 60/11 perc).

Ha csak a perceket vesszük figyelembe, akkor ez azt jelenti, hogy

m + 160/11 = 60l/11 + 60s,

ahol s lehet negatív egész is. Ebből

11m + 160 = 60l + 660s

következik. Ez utóbbi egyenletből egyrészt 20|m, másrészt 3|11m+160, amiből m=40. Tehát 11^.40+160=600=60l+660s, vagyis 10=l+11s. Ha s<0, akkor l>11, ami nem lehet. Ha s=0, akkor pedig l=10.

Tehát a 10. átfedéskor pillantott órájára a vezető, vagyis a vonat (délelőtt vagy este) 10^.(1 óra 60/11 perc) - 14 6/11 perc = 10 óra 40 perckor indult.

C.751.Egy deltoid oldalai a és b (a$\displaystyle \ne$b). A különböző hosszúságú oldalak derékszöget zárnak be. Mekkora annak a körnek a sugara, amely a deltoid mind a négy oldalának meghosszabbítását érinti?

Megoldás: Legyen mondjuk b>a. Ekkor a következő ábrát kapjuk:

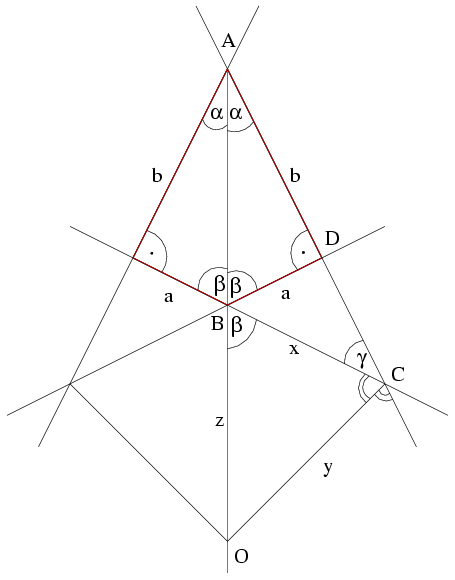
A BOC háromszög x oldalához tartozó m magasságát keressük. A BCD háromszögből a/x=sin $\displaystyle \gamma$=sin (90^o-2$\displaystyle \alpha$), vagyis x=a/(sin (90^o-2$\displaystyle \alpha$)).

Térjünk át a BOC háromszögre.

BCO$\displaystyle \angle$=(180^o-$\displaystyle \gamma$)/2=(180^o-(90^o-2$\displaystyle \alpha$))/2=45^o+$\displaystyle \alpha$.

BOC$\displaystyle \angle$=180^o-$\displaystyle \beta$-(45^o+$\displaystyle \alpha$)=180^o-(90^o-$\displaystyle \alpha$)-(45^o+$\displaystyle \alpha$)=45^o.

Ezután fölírhatjuk a szinusz-tételt az y és az x oldalakra:

$\displaystyle y:{a\over\sin(90^{\circ}-2\alpha)}=\sin\beta:\sin45^{\circ}$

$\displaystyle y={\sin\beta\cdot a\over\sin45^{\circ}\cdot\sin(90^{\circ}-2\alpha)}= {\sin(90^{\circ}-\alpha)\cdot a\over\sin45^{\circ}\cdot\sin(90^{\circ}-2\alpha)}$

A szinusz-tételt a z és az x oldalakra fölírva:

$\displaystyle z:x={\sin(45^{\circ}+\alpha)\over\sin45^{\circ}}$

$\displaystyle z={\sin(45^{\circ}+\alpha)\cdot a\over\sin45^{\circ}\sin(90^{\circ}-2\alpha)}$

A háromszög területét kétféleképpen felírva $\displaystyle xm=zy\sin45^{\circ}=zy{\sqrt2\over2}$, ahonnan

$\displaystyle m={zy\sqrt2\over2x}={\sin\beta\sin(45^{\circ}+\alpha)\cdot a^2\sin(90^{\circ}-2\alpha)\cdot\sqrt2\over2\cdot1/2\cdot\sin^2(90^{\circ}-2\alpha)\cdot a}=$

$\displaystyle =\sqrt2a{\sin(90^{\circ}-\alpha)\sin(45^{\circ}+\alpha)\over\sin(90^{\circ}-2\alpha)}= \sqrt2a{\cos(-\alpha)\cdot(\sqrt2/2)(\cos\alpha+\sin\alpha)\over\cos(-2\alpha)}=$

$\displaystyle =a\cdot{\cos^2\alpha+\cos\alpha\sin\alpha\over2cos^2\alpha-1}.$

Felhasználva, hogy a/b=tan $\displaystyle \alpha$, illetve $\displaystyle \cos\alpha=b/\sqrt{a^2+b^2}$ és így $\displaystyle \cos^2\alpha={b^2\over a^2+b^2}$, kapjuk, hogy

$\displaystyle m=a\cdot{1+\sin\alpha/\cos\alpha\over2-1/\cos^2\alpha}=a\cdot{1+a/b\over2-(a^2+b^2)/b^2}=a\cdot{1+a/b\over1-(a/b)^2}=a\cdot{b^2+ab\over b^2-a^2}={ab(a+b)\over(b-a)(a+b)}={ab\over b-a}.$

C.752.Igazoljuk, hogy ha az a, b, c pozitív számok egy mértani sorozat egymást követő elemei, akkor az a+b+c, $\displaystyle \sqrt{3(ab+bc+ca)}$ és $\displaystyle \root3\of{27abc}$ is egy mértani sorozat elemei.

Megoldás: Legyen például a=b/q és c=bq. Ekkor

$\displaystyle a+b+c={b\over q}+b+bq=b\left({1\over q}+1+q\right),$

$\displaystyle \sqrt{3(ab+bc+ca)}=\sqrt{3\left({b^2\over q}+b^2q+b^2\right)}= \sqrt{3b^2\left({1\over q}+1+q\right)},$

$\displaystyle \root3\of{27abc}=3\root3\of{b^3}=3b.$

Ekkor viszont

$\displaystyle {b\left({1\over q}+1+q\right)\over\sqrt{3b^2\left({1\over q}+1+q\right)}}= {\sqrt{3b^2\left({1\over q}+1+q\right)}\over3b},$

hiszen ez ekvivalens a következő nyilvánvaló egyenlőséggel:

$\displaystyle {\sqrt{{1\over q}+1+q}\over\sqrt3}={\sqrt3\over3}\sqrt{{1\over q}+1+q}.$

Vagyis valóban

$\displaystyle {a+b+c\over\sqrt{3(ab+bc+ca)}}={\sqrt{3(ab+bc+ca)}\over\root3\of{27abc}}.$

C.753.Másfél literes ásványvizes palackok övszerűen el vannak keskenyítve, hogy jobban meg lehessen őket fogni. A palack normál kerülete 27,5 cm, a derekánál - ami 1 cm magas hengerpalást - csak 21,6 cm. A különböző kerületű hengerpalástokat az öv felett és alatt egyaránt 2 cm magas csonkakúp palástok kötik össze. Mennyivel magasabbak az ilyen palackok, mint az ugyanolyan űrtartalmú és normál kerületű, öv nélküli társaik?

Megoldás: Egy öves palack elkeskenyített részének magassága 5 cm. Számítsuk ki ennek a résznek a térfogatát, majd nézzük meg, hogy ugyanekkora térfogatot egy öv nélküli palack mekkora magasságú része ad ki. (Ezt a magasságot M-mel jelöljük.)

A palack normál sugara: $\displaystyle r={27,5\over2\pi}$. Az öv sugara: $\displaystyle r_2={21,6\over2\pi}$. Az öv térfogata $\displaystyle r_2^2\pi\cdot1={466,56\over4\pi}={1399,68\over12\pi}$. A két csonkakúp térfogata összesen:

$\displaystyle {4\pi\over3}\left({27,5^2\over4\pi^2}+{21,6^2\over4\pi^2}+{21,6\cdot27,5\over4\pi^2}\right)= {1816,81\over3\pi}={7267,24\over12\pi}.$

Az együttes térfogat ezek összege, azaz:

$\displaystyle {8666,92\over12\pi}=r^2\pi\cdot M={27,5^2\over4\pi^2}\pi\cdot M={2268,75\over12\pi}M$. Ebből M$\displaystyle \approx$3,82. Tehát egy elkeskenyített palack 5-M$\displaystyle \approx$5-3,82=1,18 cm-rel magasabb öv nélküli társainál.

C.754.Oldjuk meg a $\displaystyle \frac{2003x}{2004}=2003^{\log_x2004}$ egyenletet.

Megoldás: Vizsgáljuk meg először, mi a helyzet x>1 esetén. Ekkor x=2004 nyilván megoldás. Ha x>2004, akkor az egyenlet baloldala nő, míg jobboldala csökken. Hasonlóan, ha x<2004, akkor pedig a jobboldal nő és a baloldal csökken. Újabb megoldást tehát egyik esetben sem kaphatunk.

Keressünk x<1 esetén megoldást. A baloldalon $\displaystyle x={1\over2003}$ esetén viszonylag egyszerű értéket kapunk, $\displaystyle {1\over2004}$-et. Nézzük, mit kapunk a jobboldalon.

$\displaystyle 2003^{\log_{1/2003}2004}=2003^{-\log_{2003}2004}=\left(2003^{\log_{2003}2004}\right)^{-1}={1\over2004}.$

Tehát x=1/2003 is megoldás. Ha 0<x<1/2003, akkor a baloldal csökken, míg a jobboldal nő. Ha pedig 1/2003<x<1, akkor a baloldal nő és a jobboldal csökken.

Tehát két megoldást kaptunk: x₁=2004, x₂=1/2003.