A 2004. áprilisi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C.760.Egy üzletben 1000 forintossal fizettünk. A blokkon a fizetendő és a visszajáró összeg ugyanazokból a számjegyekből állt, csak más sorrendben. Mennyi a számjegyek összege?

Megoldás: Csak háromjegyű számról lehet szó. A lehetőségek:

1.) \(\displaystyle \overline{abc}+\overline{acb}=100\)

Ebből c+b=10, b+c=9, ami ellentmondás.

2.) \(\displaystyle \overline{abc}+\overline{bac}=100\)

Ebből 2c=10, c=5, a=b=9. Hat ilyen szám van, mindben 14 a számjegyek összege.

3.) \(\displaystyle \overline{abc}+\overline{bca}=100\)

Ebből c+a=10, b+c=9, a+b=9, vagyis a=c=5, b=4. A számjegyek összege ekkor is 14.

4.) \(\displaystyle \overline{abc}+\overline{cab}=100\)

Ez megegyezik az előző esettel, csak a betűk szerepe cserélődött fel.

5.) \(\displaystyle \overline{abc}+\overline{cba}=100\)

a+c=10, 2b=9. Ez utóbbi nem lehet.

Vagyis a számjegyek összege minden lehetséges esetben 14.

C.761.Egy háromszög két oldalának hossza adott, továbbá tudjuk, hogy az ezekhez tartozó súlyvonalak merőlegesek egymásra. Számítsuk ki a harmadik oldal hosszát.

Megoldás:

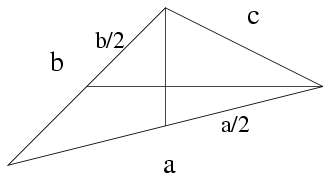
A Pitagorasz tételből

\(\displaystyle \left({a\over2}\right)^2=\left({s_a\over3}\right)^2+\left({2\over3}s_b\right)^2\)

\(\displaystyle \left({b\over2}\right)^2=\left({s_b\over3}\right)^2+\left({2\over3}s_a\right)^2\)

Ebből 4s_b²=2,4a²-0,6b² és 16s_a²=9,6b²-2,4a². Innen

\(\displaystyle c^2=\left({2\over3}s_b\right)^2+\left({2\over3}s_a\right)^2= {a^2+b^2\over5}.\)

C.762.A K₁ kocka körülírt gömbjének a felszíne kétszer akkora, mint a K₂ kocka beírt gömbjének a felszíne. Jelölje V₁ a K₁ kocka beírt gömbjének a térfogatát, V₂ pedig a K₂ kocka körülírt gömbjének a térfogatát. Mekkora a \(\displaystyle \frac{V_1}{V_2}\) arány?

Megoldás: Ha egy kocka oldala a, akkor a köré írható gömb sugara \(\displaystyle R={\sqrt3\over2}a\), a beleírt gömbé pedig \(\displaystyle r={1\over2}a\). Jelölje K₁ köréírt gömjének sugarát R₁, K₂-ét R₂, a beírt gömbök sugarát pedig r₁ és r₂. Tudjuk, hogy \(\displaystyle {R_1^2\over r_2^2}=2\), és keressük a \(\displaystyle {V_1\over V_2}\) arányt.

\(\displaystyle {\left({\sqrt3\over2}a_1^2\right)\over\left({1\over2}a_2^2\right)}=2,\)

ebből \(\displaystyle a_1=a_2\sqrt{2/3}\).

\(\displaystyle {V_1\over V_2}={r_1^3\over R_2^3}={\left({1\over2}a_1\right)^3\over\left({\sqrt3\over2}a_2^3\right)}={\left({1\over2}a_2\sqrt{{2\over3}}\right)^3\over\left({\sqrt3\over2}a_2\right)^3}={2\sqrt2\over27}. \)

C.763.Egy sarokban lévő állványon három, 30 cm x40 cm-es polc van, a szomszédosak távolsága egyenlő. Ahol a két fal és a középső polc találkozik, három pók tanyázott. Egyszer egyikük az egyik falon ferdén felmászott a felső polc sarkához, másikuk a másik falon ferdén lemászott az alsó polc sarkához. A harmadik pók a helyén maradt, és megállapította, hogy arról a helyről társai 120^o-os szögben látszanak. Mekkora a polcok távolsága? (A szomszédos polcok ugyanakkora távolságra vannak egymástól.)

Megoldás:

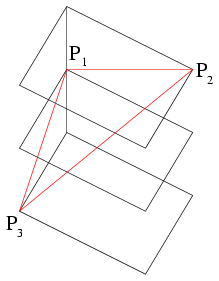
A polcok távolságát m-mel jelölve \(\displaystyle P_3P_1=\sqrt{m^2+30^2}\), \(\displaystyle P_1P_2=\sqrt{m^2+40^2}\) és \(\displaystyle P_3P_2=\sqrt{4m^2+30^2+40^2}\). Mivel P₃P₁P₂\(\displaystyle \angle\)=120^o, ezért a P₁P₂P₃ háromszögre felírva a koszinuszt tételt azt kapjuk, hogy

\(\displaystyle 4m^2+2500=2m^2+2500-2\sqrt{(m^2+900)(m^2+1600)}\cdot(-0,5).\)

Ebből m²\(\displaystyle \approx\)1225,13 (a másik érték negatív lenne), amiből m\(\displaystyle \approx\)35.

C.764.Adott az s valós szám. Oldjuk meg a

\(\displaystyle \log_{\frac{1}{s}}\log_s\)\log_s\log_sx ">

egyenlőtlenséget.

Megoldás: Felhasználva, hogy log_1/ab=-log_ab, az egyenlőtlenség ekvivalens azzal, hogy

-log_slog_sx>log_slog_sx,

ami pontosan akkor teljesül, hogyha log_slog_sx<0. Két eset van. Mindkét esetben értelmesnek kell lennie a feladatban szereplő kifejezéseknek, vagyis s>0, s\(\displaystyle \ne\)1; log_s x>0.

I.) s>1, így log_s x>0 miatt x>1. Ekkor log_s x<1, vagyis 1<x<s.

II.) 0<s<1, így log_s x>0 miatt 0<x<1. Ekkor log_s x>1, vagyis 0<x<s.