 |
A 2005. januári K-jelű matematika gyakorlatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
K. 25. Az ábrán egy városrész térképvázlata látható. A körök az utcasarkokat (kereszteződéseket), a vonalak az őket összekötő útszakaszokat jelzik. Minden útszakasznál feltüntettük, hogy gyalog hány perc alatt tehetők meg. Mennyi a lehetséges legkisebb időtartam, amely ahhoz szükséges, hogy eljussunk A pontból B pontba, feltéve, hogy az ábrán mindig csak jobbra vagy felfelé haladunk?
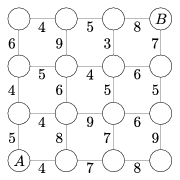
Megoldás: A leggyorsabb utat a legegyszerűbben úgy kaphatjuk meg, ha B-ből visszafelé indulva minden körbe beírjuk, hogy onnan legkevesebb mennyi idő alatt lehet megközelíteni B-t. Így sorban haladva, és mindig felhasználva a korábban egy adott kereszteződésre megállapított minimális értéket, az alábbi ábrát kapjuk:
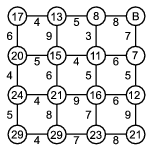
Tehát a lehető leggyorsabb út 29 perc, és ez az alábbi útvonallal érhető el:
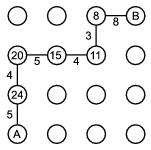
Megjegyzés: Ha A-ból kiindulva az úgynevezett ,,mohó algoritmus'' alapján minden kereszteződésnél a leggyorsabb utat választjuk, akkor 34 perc alatt érünk A-ból B-be. Az ennek megfelelő út az ábrán látható. Azonban korábban már láthattuk, hogy nem ez a leggyorsabb út.
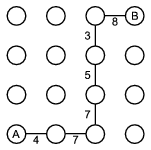
K. 26. Sanyi és apja beszélgetnek:
- Fiam, hány oldalas a könyv, amit el kell olvasnod?
- 1000-nél kevesebb.
- Elkezdted már?
- Igen, vasárnap már túl is jutottam a százötvenedik oldalon.
- És ma mennyit haladtál?
- Nagyon sokat! A ma olvasott oldalak sorszámának 2761 az összege.
A beszélgetés napján hányadik oldalon kezdte az olvasást, és hány oldalt olvasott Sanyi?
Megoldás: Legyen x + 1 a sorszáma az első ma olvasott oldalnak, és jelölje k az elolvasott oldalak számát. Ekkor a szöveg alapján az alábbi összefüggést írhatjuk fel: x+1+x+2+...+x+k=2761. Végezzük el az összegzéseket pl. Gauss módszerével: \(\displaystyle kx+{k(k+1)\over2}=2761\), majd mindkét oldalt szorozzuk meg 2-vel: k(2x+k+1)=5522. Mivel 5522 prímtényezős felbontása 2.11.251, és a bal oldal két tényezője közül k a kisebbik, ezért az alábbi lehetséges értékek adódnak:
| k | 1 | 2 | 11 | 22 |
| 2x+k+1 | 5522 | 2761 | 502 | 251 |
| x | 2760 | 1379 | 245 | 114 |
Mivel Sanyi már túl van a 150. oldalon, ezért csak a 246. oldalon kezdhette az olvasást, és így 11 oldalt olvasott el a beszélgetés napján.
K. 27. Van-e olyan legalább kétjegyű négyzetszám, amelyik különböző számjegyekből áll, és igaz rá, hogy számjegyeit bármilyen sorrendben írjuk le, a kapott szám is négyzetszám?
Halász Tamás (Budapest) javaslata alapján
Megoldás: A négyzetszámok végződése csak hatféle lehet: 0, 1, 4, 5, 6, 9. Mivel 0-val nem kezdődhet szám, ezért a 0 kiesik a lehetséges számjegyek közül. 5 sem szerepelhet a számban, hiszen az 5-re végződő négyzetszámok oszthatók 5-tel, tehát 25-tel is, így utolsó előtti számjegyük 2, ez viszont nem szerepel a lehetőségek között. Maradnak tehát azok a számok, melyek az 1, 4, 6, 9 számjegyek közül valahányat tartalmaznak. Négyjegyű számot képezve ezekből nem kapunk megoldást, mert pl. 1946 nem négyzetszám. Háromjegyű számokat képezve sem kapunk megoldást, mert 146, 149, 916, 469 egyike sem négyzetszám. Maradnak tehát az említett számjegyekből összeállítható kétjegyű számok, de ezek sem adnak megoldást, mert 14, 61, 19, 46, 94, 69 egyike sem négyzetszám. Tehát nincs a feltételeknek megfelelő négyzetszám.
K. 28. Adjuk meg az összes olyan p prímszámot, amelyre 2p2 +13 is prímszám.
Megoldás: A p = 3 megoldás. Ha p nem 3, akkor 2p2+13 = 2(p2-1)+15 = 2(p-1)(p+1)+15 osztható 3-mal (és nem 3), ezért nem lehet prím. Tehát p-nek csak egy lehetséges értéke van, a 3.
K. 29. Bizonyítsuk be, hogy ha a 121 szám jegyei közé mindkét helyen ugyanannyi nullát írunk (pl. 10 201, 1 002 001 stb.), akkor mindig egy egész szám négyzetét kapjuk.
Megoldás: Ha az 1 és 2, valamint a 2 és 1 közé k db 0-t írunk be, akkor a kapott szám: 102k+2+2.10k+1+1 = (10k+1+1)2, tehát tényleg négyzetszámot kapunk.
K. 30. Igazoljuk, hogy egy tetszőleges konvex négyszög átlóinak összege nagyobb, mint a kerületének a fele, de kisebb, mint a kerülete.
Megoldás: Tekintsünk egy konvex négyszöget:
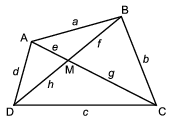
Jelöljük az átlók metszéspontjától a csúcsokig húzott szakaszok hosszát az ábrának megfelelően e, f, g, h-val. Írjuk fel a háromszög-egyenlőtlenséget az ábrán látható négy kis háromszögben: a < e + f, b < f + g, c < g + h, d < h + e. A kapott egyenlőtlenségeket összeadva a + b + c + d < 2(e + f + g + h). A bal oldalon a kerület, a jobb oldalon az átlók összhosszának kétszerese látható, melyből 2-vel való osztás után kapjuk az első bizonyítandó állítást. A második állítás bizonyításához írjuk fel a háromszög-egyenlőtlenséget az ABD, ABC, BCD, CDA háromszögekben: a + d > h + f, a + b > e + g, b + c > h + f, c + d > e + g. Az egyenlőtlenségeket összeadva, és a kapott egyenlőtlenség mindkét oldalát 2-vel osztva az a + b + c + d > e + f + g + h egyenlőtlenséget kapjuk, ami éppen a második bizonyítandó állítás.

