Matematikából kitűzött gyakorlatok és feladatok
2005. január

Kérjük, olvassa el a versenykiírást.

A K pontversenyben kitűzött gyakorlatok A K-jelű feladatokat csak 9-edik osztályosok küldhetik be. Minden K-jelű feladat helyes megoldásáért 6 pont jár.

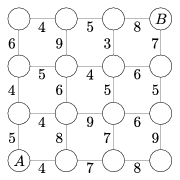
K. 25. Az ábrán egy városrész térképvázlata látható. A körök az utcasarkokat (kereszteződéseket), a vonalak az őket összekötő útszakaszokat jelzik. Minden útszakasznál feltüntettük, hogy gyalog hány perc alatt tehetők meg. Mennyi a lehetséges legkisebb időtartam, amely ahhoz szükséges, hogy eljussunk A pontból B pontba, feltéve, hogy az ábrán mindig csak jobbra vagy felfelé haladunk?

K. 26. Sanyi és apja beszélgetnek:

- Fiam, hány oldalas a könyv, amit el kell olvasnod?

- 1000-nél kevesebb.

- Elkezdted már?

- Igen, vasárnap már túl is jutottam a százötvenedik oldalon.

- És ma mennyit haladtál?

- Nagyon sokat! A ma olvasott oldalak sorszámának 2761 az összege.

A beszélgetés napján hányadik oldalon kezdte az olvasást, és hány oldalt olvasott Sanyi?

K. 27. Van-e olyan legalább kétjegyű négyzetszám, amelyik különböző számjegyekből áll, és igaz rá, hogy számjegyeit bármilyen sorrendben írjuk le, a kapott szám is négyzetszám?

Halász Tamás (Budapest) javaslata alapján

K. 28. Adjuk meg az összes olyan p prímszámot, amelyre 2p² +13 is prímszám.

K. 29. Bizonyítsuk be, hogy ha a 121 szám jegyei közé mindkét helyen ugyanannyi nullát írunk (pl. 10 201, 1 002 001 stb.), akkor mindig egy egész szám négyzetét kapjuk.

K. 30. Igazoljuk, hogy egy tetszőleges konvex négyszög átlóinak összege nagyobb, mint a kerületének a fele, de kisebb, mint a kerülete.

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

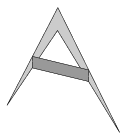
C. 790. Egy konkáv négyszög oldalainak felezőpontjait összekötöttük az ábrán látható módon. Hogyan aránylik az így kapott négyszög területe az eredeti négyszög területéhez?

C. 791. Egy 9-szer 9-es táblázat mezőibe 460-tól 540-ig beírtuk egymás után az egész számokat a bal felső sarokból indulva, soronként balról jobbra haladva. Elhelyezhető-e ezen a táblán egy négy négyzetből álló, L betűt formázó kartonlap úgy, hogy 4 olyan számot fedjen le, amelyek összege 2005?

C. 792. Oldjuk meg a következő egyenlőtlenséget:

$\displaystyle \sqrt{x^2+x}+x<\frac{1}{2}.$

C. 793. Mennyi

$\displaystyle \sqrt[4010]{\frac{1}{2}\big(19+6\sqrt{10}\,\big)}\cdot\sqrt[2005]{3\sqrt{2}- 2\sqrt{5}}$

pontos értéke?

C. 794. Egy gömb két párhuzamos síkmetszetének területe 9$\displaystyle \pi$ és 16$\displaystyle \pi$. A síkok távolsága egységnyi. Mekkora a gömb felszíne?

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3782. Az $\displaystyle A=\overline{xyzu}$ és a $\displaystyle B=\overline{uzyx}$ tízes számrendszerben felírt négyjegyű számok szorzatának utolsó három számjegye 0. Keressük meg az összes ilyen tulajdonságú A, B számpárt.

(3 pont)

B. 3783. Az ABCDE konvex ötszögben ABC$\displaystyle \angle$= CDE$\displaystyle \angle$= 90^o, BC=CD=AE=1, AB + ED = 1. Mekkora az ötszög területe?

(3 pont)

B. 3784. Igazoljuk, hogy ha a, b, c pozitív számok, akkor

$\displaystyle 6a+4b+5c\ge5\sqrt{ab}+7\sqrt{ac}+3\sqrt{bc}.$

(3 pont)

B. 3785. Egy számot szerencsésnek nevezünk, ha előáll olyan pozitív egészek összegeként, amelyek reciprokösszege 1. A 11 = 2 + 3 + 6 és a 4 = 2 + 2 például szerencsés számok, hiszen

$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{6}=\frac{1}{2}+\frac{1}{2}=1.$

Szerencsés szám-e a 2005?

(4 pont)

B. 3786. Adott 200 darab különböző valós szám. A számokat két csoportra osztjuk és mindkét csoportban nagyság szerint növekvően rendezzük az elemeket. Így kapjuk az a₁<a₂<...<a₁₀₀ és a b₁<b₂<...<b₁₀₀ sorozatokat. Ugyanezekből a számokból két újabb rendezett százas csoportot készítve az a₁'<a₂'< ...<a₁₀₀' és a b₁'<b₂'<...<b₁₀₀' sorozatokat kapjuk.

Bizonyítsuk be, hogy

|a₁-a₁'|+|a₂-a₂'|+...+|a₁₀₀-a₁₀₀'|=|b₁-b₁'|+|b₂-b₂'|+...+|b₁₀₀-b₁₀₀'|.

(5 pont)

B. 3787. Az ABC háromszög belső pontja K, az AK, BK, CK egyenesek az A₁, B₁, C₁ pontokban metszik a szemközti oldalakat. Bizonyítsuk be, hogy

$\displaystyle \frac{AK}{KA_1}+\frac{BK}{KB_1}+\frac{CK}{KC_1}\ge6.$

(4 pont)

B. 3788. Adott az ABC háromszög. Mi azon P pontok mértani helye a háromszög belsejében, amelyeknek az AB oldal egyenesétől mért távolsága számtani közepe a BC és a CA oldalak egyenesétől mért távolságának?

(4 pont)

B. 3789. Hány olyan sík van, amely egy kockának legalább három élfelező pontján átmegy?

(4 pont)

B. 3790. Oldjuk meg a következő egyenletrendszert:

$\displaystyle x^2-4\sqrt{3x-2}+10=2y,$

$\displaystyle y^2-6\sqrt{4y-3}+11=x.$

(5 pont)

Javasolta: Lorántfy László, Dabas

B. 3791. A hegyesszögű ABC háromszög belsejében levő P pontra igaz, hogy APB$\displaystyle \angle$=BPC$\displaystyle \angle$= CPA$\displaystyle \angle$. A BP és CP egyenesek az AC és AB oldalakat rendre D-ben és E-ben metszik. Mutassuk meg, hogy AB+AC$\displaystyle \ge$4DE.

(5 pont)

Olimpiai válogatóverseny feladata

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 362. Az x₁, x₂,..., x_n valós számokról tudjuk, hogy

$\displaystyle \sum_{i=1}^nx_i\ge n\quad\mbox{és}\quad\sum_{i=1}^nx_i^2\ge n^2,$

ahol n$\displaystyle \ge$3. Mutassuk meg, hogy max  (x₁, x₂,..., x_n)$\displaystyle \ge$2.

A. 363. Ki lehet-e rakni a 2005 oldalú kockát 2, 3 és 7 oldalú kockák felhasználásával?

Javasolta: Egri Attila, Hajdúszoboszló

A. 364. Adott a 25!-nak 19 osztója. Bizonyítsuk be, hogy található közöttük néhány úgy, hogy a szorzatuk köbszám.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő:

A K-jelű feladatoknál 2005. február 10.,

Az A-, B- és C-jelű feladatoknál 2005. február 15., kivéve a C.792., C.793. és B.3785. feladatokat, ezek határideje egy hónappal csúszik.