Matematikából kitűzött gyakorlatok és feladatok
2005. február
Kérjük, olvassa el a versenykiírást.
 |
A K pontversenyben kitűzött gyakorlatokA K-jelű feladatokat csak 9-edik osztályosok küldhetik be. Minden K-jelű feladat helyes megoldásáért 6 pont jár. |
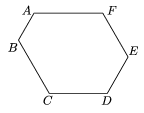
K. 31. Az ábrán látható hatszög minden belső szöge 120o-os. Bizonyítsuk be, hogy
AB + FA = CD + DE.
K. 32. Egy könyvtárban a következő módon választ 3 gyerek 5 féle könyv közül: az 5 féle könyv mindegyikéből egy-egy példány van egymás mellé kitéve egy asztalra, a gyerekek pedig arra a könyvre teszik az olvasójegyüket, amelyiket ki szeretnék kölcsönözni (egyféle könyvet többen is kölcsönözhetnek, akár mind a hárman, ilyenkor több olvasójegy kerül ugyanazon könyvre, ám egy gyerek csak egy könyvet kölcsönözhet). Két olvasójegy-elrendezés különbözőnek számít, ha legalább egy gyerek nem ugyanazt a könyvet jelölte meg a két elrendezésben. Hány lehetőségük van összesen az olvasójegyek elhelyezésére?
K. 33. Balázsnak van 11 darab műanyag hengere. Ha magasságuk szerint sorba rakja ezeket (a ,,talpukra'' állítva), akkor mindegyik 2 cm-rel nagyobb, mint az azt megelőző. A sorban a legutolsó henger éppen akkora, mint a középső és annak egyik szomszédja egymásra téve. Milyen magas oszlopot lehet építeni a 11 hengert egymásra téve?
K. 34. Oldjuk meg a következő egyenletet:
(x2-4)2 (x+3)2+ (x+2)2(x-9)2=0.
K. 35. Tudjuk, hogy a háromszög súlyvonalai felezik a területét, valamint, hogy egy ponton, a súlyponton haladnak át. Igaz-e, hogy azok a területfelező egyenesek, amelyek párhuzamosak a háromszög valamelyik oldalával, áthaladnak a háromszög súlypontján?
K. 36. Hány olyan, legalább kétjegyű egész szám van, és melyek ezek, melyekre teljesül, hogy 6 milliónál kisebbek, és az őket megelőző, valamint az őket követő egész szám is palindrom? (Palindrom számnak azokat az egész számokat nevezzük, melyek számjegyeit fordított sorrendben írva az eredeti számot kapjuk.)
 |
A C pontversenyben kitűzött gyakorlatokMinden C-jelű feladat helyes megoldásáért 5 pont jár. |
C. 795. Bizonyítsuk be, hogy ha a 10-es számrendszerben felírt \(\displaystyle \overline{a_1a_2a_3a_4a_5a_6}\) szám osztható 7-tel, akkor \(\displaystyle \overline{a_6a_1a_2a_3a_4a_5}\) is osztható 7-tel.
C. 796. Egy derékszögű háromszög beírható körének sugara az átfogóhoz tartozó magasság 0,45-szorosa. Mekkorák a háromszög hegyesszögei?
C. 797. Egy négyzet alakú étkezőasztal lábainak hossza valamilyen körüljárás szerinti sorrendben 70 cm, 71 cm, 72,5 cm és 72 cm. Billeg-e az asztal, vagyis van-e két olyan asztalláb, amely soha nem támaszkodik egyszerre a padló síkjára?
C. 798. Oldjuk meg az alábbi egyenletet:
3.4x+(3x-10)2x+3-x=0.
C. 799. Egy tetraéder minden csúcsában ül egy-egy hangya. Egy adott pillanatban mindegyikük elindul egy véletlenszerűen kiválasztott élen, és átmászik rajta a szomszédos csúcsba. Mennyi annak a valószínűsége, hogy két hangya találkozik útközben vagy az út végén?
 |
A B pontversenyben kitűzött feladatokA B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe. |
B. 3792. Az M pozitív egészből a tőle különböző N pozitív egész úgy származtatható, hogy M jegyeit valamilyen más sorrendben írjuk fel (első jegyük nem lehet nulla). Lehet-e mindkét szám a 2-nek pozitív egész kitevőjű hatványa?
(4 pont)
B. 3793. Az ABCD négyzet belsejében adott a P pont. Tudjuk, hogy AP=1, BP=2, CP=3. Határozzuk meg a DP távolságot.
(3 pont)
B. 3794. Bizonyítsuk be, hogy ha 0<q<p<1, akkor
p+3q<1+4pq.
(3 pont)
B. 3795. Adott két pont, amelyek távolsága 1 egység. Csak körző segítségével szerkesszünk két olyan pontot, amelyek távolsága \(\displaystyle \sqrt{2}\) egység.
(5 pont)
B. 3796. A k körhöz a külső A pontból érintőket húzunk, az érintési pontok E és F, az EF szakasz felezőpontja G. Egy A-n átmenő egyenes a B, C pontokban metszi a k kört. Bizonyítsuk be, hogy az EF egyenes felezi a BGC szöget.
(4 pont)
B. 3797. Adott az ABC szabályos háromszög. Mi azon P pontok mértani helye a háromszög belsejében, amelyeknek az AB oldaltól mért távolsága mértani közepe a BC és a CA oldaltól mért távolságának?
(4 pont)
B. 3798. Legyen \(\displaystyle \alpha=2+\sqrt{3}\). Bizonyítsuk be, hogy minden pozitív egész n-re
[\(\displaystyle \alpha\)n]=\(\displaystyle \alpha\)n+\(\displaystyle \alpha\)-n-1.
(4 pont)
B. 3799. Két egybevágó szabályos háromszög közös része egy hatszög. Bizonyítsuk be, hogy ebben a hatszögben a másodszomszédos oldalak hosszának összege egyenlő.
(4 pont)
B. 3800. Egy kocka minden csúcsában ül egy-egy hangya. Egy adott pillanatban mindegyikük elindul egy véletlenszerűen kiválasztott élen, és átmászik rajta a szomszédos csúcsba. Mennyi annak a valószínűsége, hogy két hangya találkozik útközben vagy az út végén?
(4 pont)
B. 3801. Jelölje P(n) az első n pozitív prímszám összegét. Bizonyítsuk be, hogy P(n) és P(n+ 1) között van négyzetszám.
(5 pont)
 |
Az A pontversenyben kitűzött nehezebb feladatokMinden A-jelű feladat helyes megoldásáért 5 pont jár. |
A. 365. Legyen \(\displaystyle a_n=\sqrt[\scriptstyle n]{(n+1)!}-\sqrt[\scriptstyle n]{n!}\) . Mutassuk meg, hogy an\(\displaystyle \ge\)1 minden n-re és az an sorozat nem korlátos.
A. 366. Legyen p(n) az n partícióinak száma, r(n) azon partíciók száma, amelyekben n-t különböző páratlan számok összegére bontjuk. Mutassuk meg, hogy p(n) és r(n) paritása megegyezik.
A. 367. a) Az ABC hegyeszögű háromszög D belső pontjára fennáll, hogy
AB.BC.CA=DA.AB.BD+DB.BC .CD+DC.CA .AD.
Határozzuk meg D mértani helyét.
b) Az ABC hegyesszögű háromszög E belső pontjára teljesül, hogy
AB.BC.CA=AE2.BC+BE2.CA+CE2.AB.
Határozzuk meg az E mértani helyét.
Dobos Sándor javaslata alapján
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
- KöMaL Szerkesztőség
Budapest 112, Pf. 32. 1518
- megoldas@komal.hu (Az interneten keresztül történő
beküldésről olvassa el tájékoztatónkat)
A beküldési határidő:
A K-jelű feladatoknál 2005. március 10.,
Az A-, B- és C-jelű feladatoknál 2005. március 15., kivéve a C.792., C.793. és B.3785. feladatokat, ezek határideje egy hónappal csúszik.

