A KöMaL 2008. novemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2008. december 11-én LEJÁRT. |
M. 291. Mérjük meg különböző hőmérsékleteken (-15 oC és +40 oC között) egy 40 W-os volfrámszálas izzólámpa ellenállását! Határozzuk meg az ellenállás hőfoktényezőjét!
(Célszerű digitális ellenállásmérőt használni. Hálózati feszültséggel ne kísérletezzünk!)
Varga István
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2008. december 11-én LEJÁRT. |
P. 4104. 2 liter térfogatú, merev falú edénybe 1 kg tömegű jégtörmeléket helyezünk, majd az edényt légmentesen lezárjuk. Miközben a hőmérséklet mindvégig 0 oC marad, a jég teljesen elolvad.
Hány százalékkal változik meg az edénybe zárt levegő nyomása?
Varga István
(3 pont)
P. 4105. Négyzetes keresztmetszetű edénybe egyforma tömegű vizet, illetve olajat önthetünk. Melyik esetben hat nagyobb nyomóerő a függőleges oldallapokra?
Varga István
(4 pont)
P. 4106. Az ábrán látható lejtő alján egy támasztékhoz rugós golyóstollat nyomunk, majd hirtelen elengedjük azt. Mérési adataink szerint a golyóstoll által megtett út a lejtő 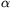 hajlásszögének függvényében:
hajlásszögének függvényében:

E táblázat alapján állapítsuk meg, mekkora kezdősebességgel indul el a golyóstoll, és mekkora a csúszási súrlódási tényező a lejtőn!
Varga István
(4 pont)
P. 4107. Vízszintes asztalon nyugvó M tömegű, R sugarú félgömbhéj aljáról lassan kimászik egy kisméretű, m tömegű bogár. Mennyi munkát végez, amíg a félgömbhéj pereméig ér? (A bogár és a félgömbhéj közötti tapadási súrlódási tényező elég nagy. A félgömbhéj tömegközéppontja kezdetben R/2 magasan van az asztal felett.)
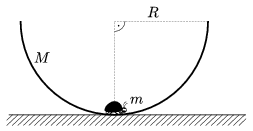
Varga István
(4 pont)
P. 4108. Egy jégkorongozó a R sugarú, m tömegű korongot v0 sebességgel üti a palánknak. A korong nem forog, a sebességvektor a palánkkal 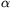 szöget zár be. A korong palánkra merőleges sebességének nagysága az ütközés során k-szorosára változik (k<1). Mekkora lesz a korong forgási energiája az ütközés után? A korong és a palánk közötti csúszási súrlódási tényező
szöget zár be. A korong palánkra merőleges sebességének nagysága az ütközés során k-szorosára változik (k<1). Mekkora lesz a korong forgási energiája az ütközés után? A korong és a palánk közötti csúszási súrlódási tényező 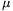 , a jégen a súrlódás elhanyagolható.
, a jégen a súrlódás elhanyagolható.
Varga István
(5 pont)
P. 4109. Van olyan játékeszköz, amelynek segítségével egyszerre igen sok, különböző méretű buborékot fújhatunk. A buborékok lassan, függőlegesen süllyednek lefelé. Feltételezve, hogy mindegyik buboréknak ugyanakkora a falvastagsága, a nagyobb, vagy a kisebb buborékok süllyednek gyorsabban?
Varga István
(4 pont)
P. 4110. Az ábrán látható 1 cm2 keresztmetszetű U alakú cső vízszintes részének hossza 10 cm, függőleges szárai pedig kellően hosszúak. A csőbe először 20 cm3 vizet töltünk, majd a bal oldali ágba szintén 20 cm3 olajat. ,
. A rendszert balra gyorsítjuk a nagyságú gyorsulással. Határozzuk meg és ábrázoljuk grafikusan a víz szintje és az olaj szintje közötti különbséget a gyorsulás függvényében!
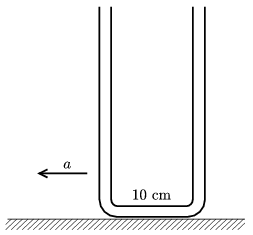
Varga István
(5 pont)
P. 4111. Egy D átmérőjű traktorkerék v sebességgel halad. A kerék peremének bármelyik részéről sárdarabok válhatnak le. Legfeljebb mennyi idő múlva eshet vissza a talajra egy sárdarab? Hol válik le a kerékről a leghosszabb ideig eső sárdarab?
Varga István
(5 pont)
P. 4112. Q töltésű, elhanyagolható kezdősebességű részecskét U feszültség gyorsít fel. A részecske B indukciójú homogén mágneses térbe jut, ahol körpályát ír le. Mekkora a ,,köráram'' mágneses nyomatéka?
Varga István
(4 pont)
P. 4113. Van de Graaff-generátor R sugarú gömbjének tetejére d vastagságú, 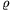 sűrűségű, r alapsugarú, alufóliából készült gömbsüveget helyezünk. Mekkora feszültségnél emelkedik fel a süveg a gömbről?
sűrűségű, r alapsugarú, alufóliából készült gömbsüveget helyezünk. Mekkora feszültségnél emelkedik fel a süveg a gömbről?
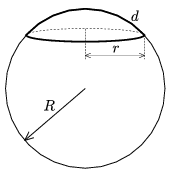
Varga István
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

