A KöMaL 2015. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. november 10-én LEJÁRT. |
M. 353. Egy sérült vagy már nem használt CD lemez közepén lévő lyukra ,,ragasszunk'' celluxszalag segítségével egy (vagy több) pénzérmét! (A lyuk átellenes oldalára is ragasszunk celluxot úgy, hogy az ottani kis bemélyedés pereme ne maradjon éles.) A lemezt - a nehezékkel lefelé fordítva - helyezzük óvatosan egy tálban lévő víz felszínére, és adott magasságból engedjünk a közepére vékony, függőleges sugárban vizet. Ha a vízhozam elegendően (de nem túlságosan) nagy, a CD lemez akkor sem süllyed el, ha elengedjük.
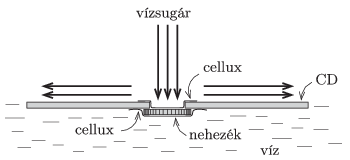
Mérjük meg, hogyan függ az ,,úszáshoz'' szükséges minimális vízhozam a lemez és a nehezék együttes tömegétől!
Közli: Baranyai Klára, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. november 10-én LEJÁRT. |
P. 4758. Milyen hosszú ellenálláshuzalt válasszunk az 1,6 \(\displaystyle \Omega\;{\rm mm}^2/{\rm m}\) fajlagos ellenállású, \(\displaystyle 0{,}1~{\rm mm}^2\) keresztmetszetű vezetékből, hogy a 230 V-os hálózatra kapcsolva 300 W-os merülőforralót készíthessünk belőle?
Közli: Holics László, Budapest
(3 pont)
P. 4759. Mekkora szöget kell bezárni két erőnek, hogy az eredőjük nagysága akkora legyen, mint a két erő nagyságának mértani közepe?
Mi a feltétele annak, hogy ez a szög minimális legyen, és mekkora ez a minimális érték?
Strasser V. Benő (1884-1966) feladata
(4 pont)
P. 4760. Egy autópályán haladó gépkocsi sebessége \(\displaystyle v_0\). Egy adott pillanatban a sebességét egyenletesen változtatni kezdi, és ettől kezdve 84 m hosszúságú utat 3 s, a következő 84 m-t 4 s alatt teszi meg.
Határozzuk meg a gépkocsi \(\displaystyle v_0\) sebességét és állandó \(\displaystyle a\) gyorsulását!
Közli: Kotek László, Pécs
(4 pont)
P. 4761. Egy érdekes jármű gyorsulása a \(\displaystyle (v_1,v_2)\) sebességintervallumban fordítottan arányos a sebességével, azaz \(\displaystyle a=A/v\) (\(\displaystyle A\) egy adott pozitív állandó).
\(\displaystyle a)\) Mennyi idő alatt gyorsul fel a jármű \(\displaystyle v_1\) sebességről \(\displaystyle v_2\)-re?
\(\displaystyle b)\) Mekkora ezalatt a jármű teljesítménye?
Közli: Sal Kristóf, Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.
(4 pont)
P. 4762. Az \(\displaystyle A_0\) keresztmetszetű fahenger aljára egy vasdarabot erősítettünk, így a fahenger stabilan úszik abban a \(\displaystyle \varrho_1\) sűrűségű folyadékban, amely egy \(\displaystyle A_1\) keresztmetszetű, hengeres főzőpohárban van. Ez a főzőpohár maga is úszik egy \(\displaystyle A_2>A_1\) keresztmetszetű másik főzőpohárban lévő \(\displaystyle \varrho_2\) sűrűségű folyadékban. E nagyobb pohár is úszik, mégpedig az \(\displaystyle A_3>A_2\) keresztmetszetű, még szélesebb főzőpohárban lévő \(\displaystyle \varrho_3\) sűrűségű folyadékban és így tovább\(\displaystyle \ldots\). Összesen \(\displaystyle n\) darab főzőpohár helyezkedik el az asztalon, mindegyik pohár tengelye és a fahengeré is függőleges.
Ezután a fahengert függőlegesen lefelé nyomjuk \(\displaystyle F\) erővel. (Sem a fahenger alja, sem a főzőpoharaké nem ér hozzá a tartóedény aljához.)
\(\displaystyle a)\) Mennyivel nő a fahenger bemerülése az első folyadékba?
\(\displaystyle b)\) Mennyivel emelkedik a folyadékszint az első főzőpohárban?
\(\displaystyle c)\) Mennyivel emelkedik a folyadékszint az \(\displaystyle i\)-edik főzőpohárban?
Közli: Lambodar Mishra, Ahmedabad, India
(5 pont)
P. 4763. Egy üvegkocka egyik lapján belépő fénysugár három olyan oldallapról verődik vissza egymás után, amelyek közös pontja a kocka valamelyik csúcsa. Ezek után a fénysugár ugyanazon a lapon lép ki a kockából, amelyen belépett.
Mit állíthatunk a kilépő fénysugár irányáról?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 4764. Az ábrán látható elektromos hálózatban minden fogyasztó ugyanakkora \(\displaystyle R\) ellenállású. Hány százalékkal változik meg az (1)-es fogyasztó teljesítménye, ha a (2)-es fogyasztót a K kapcsolóval rövidre zárjuk?
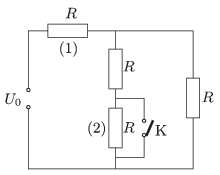
Varga István (1952-2007) feladata
(4 pont)
P. 4765. Egy 250 mH induktivitású és 0,3 \(\displaystyle \Omega\) ellenállású tekercsre egy állandó feszültségű telepet kapcsolunk. Mennyi idő múlva éri el a tekercsben folyó áram erőssége a végül beálló stacionárius érték
\(\displaystyle a)\) 50%-át;
\(\displaystyle b)\) 75%-át?
Orosz példatári feladat
(4 pont)
P. 4766. 200 nm-es ultraibolya fény világít meg egy alumíniumlemezt.
\(\displaystyle a)\) Mekkora lesz a kilépő elektronok között a leggyorsabb és a leglassabb elektron mozgási energiája?
\(\displaystyle b)\) Mekkora a zárófeszültség?
Román tankönyvi feladat
(4 pont)
P. 4767. Egy függőleges tengelyű mérőhenger falába sok apró lyukat fúrtunk. A hengert \(\displaystyle H\) magasságig feltöltjük vízzel, melynek következtében a lyukakon (a mérőhenger falára merőlegesen) vékony vízsugarak lövellnek ki. Milyen alakú a vízsugarak burkolófelülete? (A vízsugarak nem akadályozzák egymást, és folyamatos utántöltéssel gondoskodunk a hengerben a vízszint állandóságáról.)
Közli: Vigh Máté, Budapest (Kunfalvi Rezső olimpiai válogatóverseny, 2015)
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

