A KöMaL 2022. decemberi informatika feladatai

I-jelű feladatok A beküldési határidő 2023. január 16-án LEJÁRT.

---

I. 577. Egyenletesnek nevezzük azt az \(\displaystyle N\) jegyű számot, amelyben az egyes számjegyek értéke az előző helyiértéken álló számjegytől legfeljebb 1-gyel tér el.

Írjunk programot, amely egy beolvasott \(\displaystyle N\)-jegyű nem egyenletes számhoz meghatározza a nála kisebb legnagyobb és a nála nagyobb legkisebb egyenletes számot.

A program az \(\displaystyle N\)-jegyű (\(\displaystyle 2\le N\le 1\,000\,000\)) egész számot a standard bemenetről olvassa be.

A standard kimenet első sorában a beolvasott számnál kisebb legnagyobb egyenletes számot, a második sorában pedig a nála nagyobb legkisebb egyenletes számot írjuk ki.

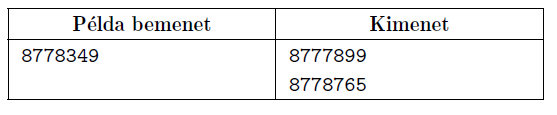
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. 5 pont kapható arra a programra, amely a \(\displaystyle 2\le N\le 1\,000\) bemenetekre helyes kimenetet ad. További 4 pont kapható a \(\displaystyle 2\le N\le 1\,000\,000\) bemenetekre 1 másodperc futásidő alatt helyes kimenetet adó programokra.

Beküldendő egy tömörített i577.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

---

I. 578. (É). A gazdaság helyzetéről rengeteget elárul a közlekedési infrastruktúra. Ebben a feladatban hazánk 2007 és 2021 közötti megyénkénti adatait fogjuk górcső alá venni.

1. Hozzunk létre a táblázatkezelőben egy új munkafüzetet. Ennek két munkalapja legyen Adatok és Valasz. Ezekre az A1-es cellától kezdve töltsük be a munkalapok nevével megegyező, UTF-8 kódolású, tabulátorral tagolt txt-fájlokat.

2. A két munkalapon végezzük el az alábbi mintákon látható formázásokat, és oldjuk meg a leírás szerinti feladatokat.

3. Az Adatok munkalapon rendezzük át a megyék adatait a megye neve szerint névsorba.

4. Az évenkénti legnagyobb fejlesztés adatait határozzuk meg a Valasz munkalap B3:G3 tartományában, tehát azt, hogy az előző évihez képest mikor és hol volt a legnagyobb növekedés, és mekkora volt a hossznövekedés értéke, mind köz-, mind vasúton.

5. Határozzuk meg a Valasz munkalap B7:G7 tartományában azt, hogy a teljes időszakra az egész országot tekintve hogyan és mennyivel változott az úthossz, mind köz-, mind vasúton. A B7 és E7 cellákban e három szöveg valamelyike szerepelhet: ,,nőtt'', ,,nem változott'' vagy ,,csökkent''.

6. A B10 és E10 cellákba azon megyék neve kerüljön, amelyeknél 2012-ben a legnagyobb volt a négyetkilométerenkénti úthossz, mind köz-, mind vasúton.

7. A B12 cellába számoljuk ki hazánk területét az adatok alapján.

8. Az A16, A17, \(\displaystyle \ldots\) cellákba kerüljön azon megyék neve, amelyekben az időszak végén, 2021-ben nem volt nagyobb a közúti és vasúti útvonalhossz összege, mint 2007-ben.

9. Feltételes formázással oldjuk meg, hogy az A16:A34 tartomány cellái közül csak azok kapjanak a minta szerinti keretet és tónust, amelyek nem üresek.

10. Egy új munkalapra készítsünk a minta szerint diagramot Békés, Csongrád–Csanád és Fejér megye közúti hosszának alakulásáról.

Az adatok forrása: a KSH
https://www.ksh.hu/stadat_files/sza/hu/sza0041.html;
https://www.ksh.hu/stadat_files/sza/hu/sza0039.html
és https://www.ksh.hu/stadat_files/fol/hu/fol0006.html oldalai.

Minták:

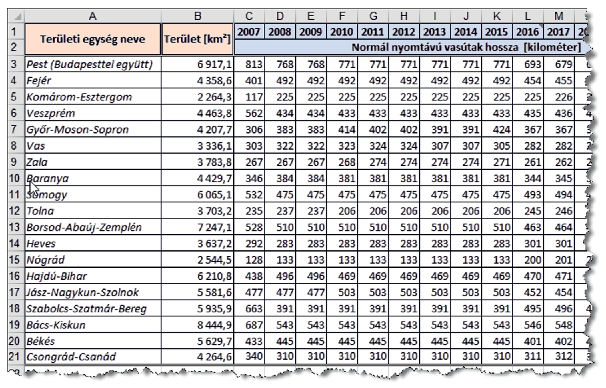
Adatok munkalap

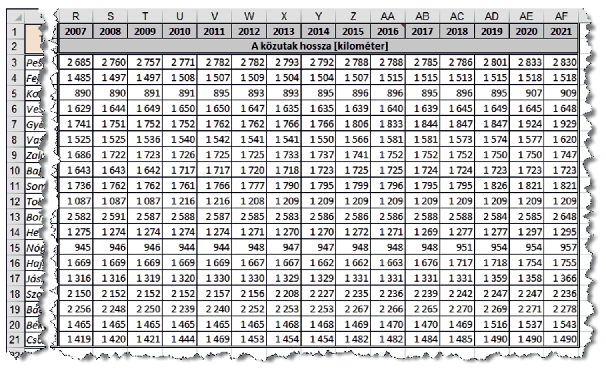
Adatok munkalap

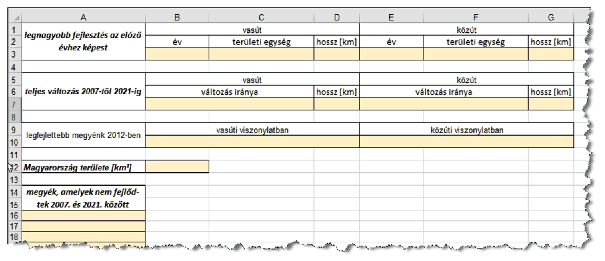
Valasz munkalap

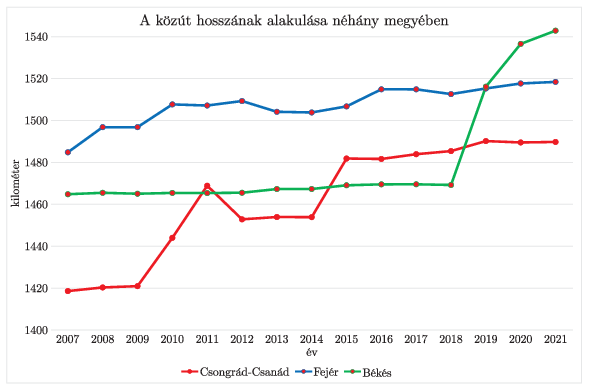
diagram

Segédszámításokat az Adatok munkalap 22. sorától lefelé vagy az AG oszloptól jobbra található cellákban végezhetünk. A megoldásban saját függvény vagy makró nem használható.

Beküldendő egy tömörített i578.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.

Letölthető állományok: adatok.txt, valasz.txt.

(10 pont)

megoldás, statisztika

---

I. 579. A Teknőcgrafika eredetileg a Logo programozási nyelvhez készült, de ma már több oktatási célú fejlesztő környezetnek és nyelvnek része, például elérhető Scratchben vagy Pythonban. Egy magyar fejlesztés keretében a Teknőcgrafikát alkalmazhatjuk a JavaScript nyelv segítségével. Az Agent JS programozási felület, valamint a dokumentáció és néhány példa található a

https://vimtaai.github.io/agent/

címen.

Különösen izgalmas területe a Teknőcgrafikának a rekurzív ábrák és fraktálok rajzolása. Készítsük el a Koch-görbe, a sárkánygörbe, valamint a Sierpiński-háromszög ábráját az Agent JS segítségével úgy, hogy a rekurzió szintje a felhasználó által beállítható legyen. A három fraktálról a KöMaL 2021. májusi számában is olvashattunk, innen származik a sárkánygörbe készítését szemléltető ábra.

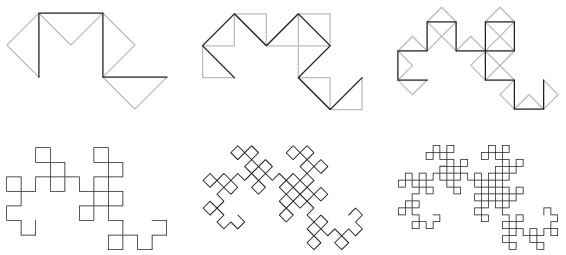
Beküldendő egy tömörített i579.zip állományban a három ábrát létrehozó oldal forráskódja.

(10 pont)

megoldás, statisztika

I/S-jelű feladatok A beküldési határidő 2023. január 16-án LEJÁRT.

---

I/S. 67. Adott egy \(\displaystyle N\times M\)-es téglalap, melyet le szeretnénk helyezni a síkra úgy, hogy az egyik csúcsa az origóba essen. Adjuk meg, hogy hányféleképpen tehetjük ezt meg úgy, hogy a másik három csúcsa is rácspontra, azaz egész koordinátákkal rendelkező pontra essen.

A bemenet egyetlen sorában az \(\displaystyle N\) és \(\displaystyle M\) számok, a téglalap oldalhosszai találhatók szóközzel elválasztva.

A kimenet egyetlen sorában egy szám szerepeljen: hányféleképpen lehet lehelyezni a téglalapot a síkra úgy, hogy az egyik csúcsa az origóba, a többi csúcsa rácspontra essen.

Példa:

Bemenet	Kimenet
2 2	4
5 10	24

Korlátok: \(\displaystyle 1 \le N,M \le 10^{6}\). Időlimit: 0,4 mp.

Értékelés: a pontok 50%-a kapható, ha a program helyes kimenetet ad az \(\displaystyle {1 \le N \le 100}\) esetekre.

Beküldendő egy is67.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2023. január 16-án LEJÁRT.

---

S. 166. Marika néni palacsintázójában egy ember süti és tölti a palacsintákat. Eddig, ha érkezett egy rendelés, akkor megsütötte a megfelelő számú palacsintát, majd beletöltötte a kért tölteléket, és odaadta a pénztárosnak, aki a fizetést elhanyagolható időn belül elintézte. Az utóbbi időben azonban nagyon népszerű lett a hely, ezért néha nagyon sokat kell várni. Hamar kiderült, hogy a sütés és palacsintatöltés közötti váltás sok időt vesz el. Azt szeretnénk kideríteni, hogy ez valóban probléma-e.

Írjunk programot, amely kiszámolja, mennyi a várakozási idők maximuma, ha minden rendelést külön-külön szolgálunk ki, illetve mennyi a várakozási idők maximumának lehető legkisebb értéke, ha pont jókor váltunk a sütés és töltés között.

Ezen a helyen nem szeretik a pazarlást, így csak akkor állnak neki egy palacsinta megsütésének, ha már van rá leadott rendelés. Tehát olyan nem fordulhat elő, hogy több megsütött palacsintánk van, mint a kiszolgálatlan rendelések összege.

A bemenet első sorában egy palacsinta megsütésének ideje S, egy palacsinta töltésének ideje \(\displaystyle T\), és a kettő közötti váltás ideje \(\displaystyle V\) szerepel. A második sorban a rendelések \(\displaystyle R\) száma van. A következő \(\displaystyle R\) sor mindegyikében két egész szám szerepel: az adott rendelés leadásának időpontja és a kért palacsinták száma.

A kimenet első sorába írjuk ki, mennyi a várakozási idők maximuma, ha a rendeléseket egyesével szolgáljuk ki, azaz mindig csak annyi palacsintát sütünk, amennyi a következő rendeléshez kell. A kimenet második sorába pedig azt, hogy mennyi a várakozási idők maximumának lehető legkisebb értéke.

Minta:

Bemenet (a / jel sortörést helyettesít)	Kimenet (a / jel sortörést helyettesít)
2 1 1 / 2 / 0 5 / 2 1	19 / 18

Magyarázat (zárójelben a befejezési idő szerepel): az első esetben megsütünk 5-öt (10), majd megtöltjük (16), majd váltunk és sütünk még egyet (19), majd azt is megtöltjük (21). A várakozási idő csökkenthető, ha előbb megsütünk 5-öt (10), majd mivel van rá rendelés, még egyet (12), majd váltunk és megtöltjük az első ötöt (18), majd még egyet (19).

Korlátok: \(\displaystyle 1\le S,T,V \le 10^4\), \(\displaystyle R \le 10^5\). A rendelés ideje és a rendelések számának összege is legfeljebb \(\displaystyle 10^5\). Időlimit: 1 mp.

Értékelés: a pontok 20%-a kapható, ha a program által adott kimenet első sora helyes. További 40% kapható, ha a program helyes kimenetet ad az \(\displaystyle R\le 10\) és a palacsinták számának összege legfeljebb 20 esetekben.

Beküldendő egy s166.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

statisztika