A Fields-éremről

Bevezetés

A négyévente megrendezésre kerülő Nemzetközi Matematikai Kongresszus legutóbbi ülését az elmúlt nyáron tartották Pekingben. A kongresszus keretében immár tizenötödik alkalommal került sor a matematikai tudomány legnagyobb szakmai elismeréseinek, a Fields-érmeknek az átadására. Ebből az alkalomból érdemes röviden áttekintenünk a díj történetét és céljait, ízelítőül néhány olyan kiemelkedő tudós munkáját is bemutatva, akit a magas kitüntetéssel jutalmaztak.

Amint az közismert, matematikai Nobel-díjat nem osztanak. Ennek okairól több legenda is kering, amelyek közül a legszórakoztatóbb az, miszerint Alfred Nobel azért orrolt volna meg a matematikára, mert az akkori idők legbefolyásosabb svéd matematikusa, Gösta Mittag-Leffler elszerette tőle a feleségét. Sajnos, az anekdotának van egy aprócska szépséghibája: Nobel sosem nősült meg. Ennek ellenére valószínűnek tűnik, hogy Nobel és Mittag-Leffler viszonya tényleg nem volt felhőtlen. Jó barátságban volt viszont Mittag-Lefflerrel (és más kiváló európai matematikusokkal) John Charles Fields kanadai matematikus, aki - minthogy szülőhazája a XX. század elején még igencsak elmaradott országnak számított a tudományos kutatás terén - szívügyének tekintette a nemzetközi matematikai kapcsolatok fejlesztését. Ezért 1931-ben ő kezdeményezte azt is, hogy - részben a Nobel-díj hiányát pótlandó - alapítsanak nemzetközi díjat a kiemelkedő teljesítményt nyújtó matematikusok jutalmazására. Elképzelése az volt, hogy a díjakat egy nemzetközi bizottság javaslatára négyévente, a Nemzetközi Matematikai Kongresszuson adják át 2-2 kutatónak (1966-tól a kitüntetethetők számát 4-ben maximálták). Fields az első, 1936-os díjkiosztást azonban már nem érhette meg, mert 1932-ben elhalálozott. Végrendeletében 46 000 akkori kanadai dollárt hagyott a díj fedezésére szolgáló nemzetközi alapítványra, ami természetesen nem mérhető Nobel hagyatékához. Ennek megfelelően a díjjal járó pénzösszeg is meglehetősen szerény: jelenleg 15 000 kanadai dollár (kb. 2,4 millió forint).

Annál nagyobb viszont a kitüntetés szakmai presztízse, amit a (változó összetételű) zsűri tagjainak és az eddigi kitüntetetteknek a tekintélye biztosít. A Nobel-díjhoz hasonlóan a Fields-érem sem életműdíj, hanem egyes kiemelkedő eredményekért ítélik oda. Van azonban egy fontos megkötés, amely megkülönbözteti a hasonló tudományos díjak többségétől: feltétel, hogy a díjazott tudós a kiemelt eredményt még 40 éves kora előtt érje el. Fields szándéka a megszorítással az volt, hogy a díj ne pusztán a teljesítmények elismerése legyen, hanem egyben ösztönzést is adjon a kitüntetettek további munkájához. Ezzel talán azt a (mindmáig) közkeletű vélekedést is el kívánta oszlatni, amely szerint a matematikusok egészen fiatalon érik el legnagyobb eredményeiket, majd pedig hamar kiégnek. A valóság ezzel szemben az, hogy a matematikusok többsége harmincas-negyvenes éveiben van alkotóereje teljében, így a Fields által meghúzott határ reálisnak tekinthető. Szándékának helyességét mi sem igazolja jobban, mint az, hogy a Fields-érmes tudósok legtöbbje később is jelentős eredményekkel gazdagította a matematikát - nem egy közülük más területeken is, mint amiért az elismerést kapta.

A korhatár azonban könyörtelen is: sok kiváló matematikus azért maradt le a Fields-éremről, mert 40 éves kora után jutott el pályája csúcsára. A leghíresebb ilyen eset Andrew Wilesé, aki a Fermat-sejtést 41 éves korában bizonyította be; hosszas vita után végül ezért a szenzációs eredményéért a Kongresszus 1998-ban személyre szóló különdíjjal jutalmazta. Ugyancsak ,,fájdalomdíjul'' szolgálhatnak a Fields-éremről lemaradt tudósok számára a különféle életműdíjak. Ezek leghíresebbike az izraeli Wolf-díj, amelynek három magyar, illetve magyar származású matematikus is kitüntetettje: a néhai Erdős Pál akadémikus, a New Yorkban élő Lax Péter professzor, és a sokáig az ELTÉ-n tanító, jelenleg a Microsoft kutatóintézetében dolgozó Lovász László akadémikus.

A Fields-érmes matematikusok névsora

Most pedig lássuk azon tudósok listáját, akik az 1936-os alapítás óta megkapták a magas kitüntetést.

[1936:] Lars Ahlfors (finn; komplex függvénytan)
Jesse Douglas (amerikai; analízis, differenciálgeometria)

[1950:] Laurent Schwartz (francia; analízis)
Atle Selberg (norvég; számelmélet)

[1954:] Kunihiko Kodaira (japán; algebrai és analitikus geometria)
Jean-Pierre Serre (francia; topológia)

[1958:] Klaus Friedrich Roth (német; számelmélet)
René Thom (francia; topológia)

[1962:] Lars Hörmander (svéd; analízis)
John Milnor (amerikai; topológia)

[1966:] Michael Francis Atiyah (brit; analízis, analitikus geometria, K-elmélet)
Paul Cohen (amerikai; halmazelmélet, matematikai logika)
Alexander Grothendieck (francia; algebrai geometria)
Stephen Smale (amerikai; topológia)

[1970:] Alan Baker (brit; számelmélet)
Heiszuke Hironaka (japán; algebrai geometria)
Szergej Novikov (orosz; topológia)
John Thompson (brit; algebra)

[1974:] Enrico Bombieri (olasz; analízis, számelmélet)
David Mumford (brit; algebrai geometria)

[1978:] Pierre Deligne (belga; algebrai geometria)
Charles Fefferman (amerikai; komplex függvénytan)
Grigorij Margulisz (orosz; differenciálgeometria, dinamikai rendszerek)
Daniel Quillen (kanadai; topológia, K-elmélet)

[1982:] Alain Connes (francia; analízis, differenciálgeometria)
William Thurston (amerikai; topológia)
Siu-Tung Yau (kínai; analízis, algebrai és analitikus geometria)

[1986:] Simon Donaldson (brit; topológia)
Gerd Faltings (német; algebrai geometria, számelmélet)
Michael Freedman (amerikai; topológia)

[1990:] Vlagyimir Drinfeld (ukrán; algebrai geometria, algebra, matematikai fizika)
Vaughan Jones (ausztrál; topológia, matematikai fizika)
Sigefumi Mori (japán; algebrai geometria)
Edward Witten (amerikai; matematikai fizika, topológia)

[1994:] Jean Bourgain (belga; analízis)
Pierre-Louis Lions (francia; analízis)
Jean-Christophe Yoccoz (francia; dinamikai rendszerek)
Jefim Zelmanov (orosz; algebra)

[1998:] Richard Borcherds (brit; algebra)
Timothy Gowers (brit; analízis, kombinatorika)
Makszim Koncevics (orosz; algebrai geometria, matematikai fizika)
Curtis McMullen (amerikai; analitikus geometria, dinamikai rendszerek)

[2002:] Laurent Lafforgue (francia; algebrai geometria)
Vlagyimir Voevodszkij (orosz; algebrai geometria, K-elmélet)

A fenti listát átböngészve először talán a díjazottak nemzeti megoszlása tűnik fel. Nem meglepő, hogy a nagy matematikus-nemzetek dominálnak: az amerikaiak, a britek, a franciák és az oroszok. Meglepő viszont egy másik nagymúltú matematikai iskola alulreprezentáltsága: a németeké. Ennek, sajnos, főként történelmi-politikai okai vannak: az első világháborús vérveszteség, a náci diktatúra és a hidegháborús megosztottság olyan súlyos károkat okoztak a német matematikának, amelyeket csak napjainkra tudott kiheverni. Szólnunk kell a magyar matematikusok hiányáról is. Nos, itt az a helyzet, hogy a XX. század elejének aranykora után a magyar matematika távolabb került a nemzetközi kutatás fősodrától; bár nagy egyéniségek továbbra is voltak, a Fields-éremmel jutalmazott tudományterületek többségének nem akadt hazai művelője. Szerencsére e téren az utóbbi évtizedben reményt keltő változások történtek, és a külföldi tanulási, utazási lehetőségek bővülésével további felzárkózás várható.

Ha a díjazottak tudományterületek szerinti megoszlását vizsgáljuk, akkor az évek során nem figyelhetünk meg számottevő hangsúlyeltolódást. Lényegében az elméleti matematika klasszikus nagy ágai: a matematikai analízis, az algebra, a számelmélet, illetve a geometria különböző válfajai (topológia, differenciálgeometria, algebrai geometria) szerepelnek kezdettől fogva a listán. Fájó pont ugyanakkor néhány fontos terület mellőzése, mint például a valószínűségelmélet teljes hiánya, vagy a matematikai logikának juttatott egyetlen Fields-érem. Ugyancsak hiányoznak olyan, az alkalmazások szempontjából jelentős területek művelői, mint a számítástudomány, a numerikus analízis és az információelmélet - az ő részükre alapította a Kongresszus 1982-ben a Rolf Nevanlinna-díjat, amelyet a Fields-érmekkel egy időben adnak át.

Ejtsünk most szót arról a kérdésről is, hogy milyen teljesítményeket jutalmaznak Fields-éremmel. Ezeket durván két csoportra oszthatjuk: híres nyitott problémák megoldására, illetve új elméletek kidolgozására. A két kategória természetesen egyáltalán nem független egymástól. Egy nevezetes sejtés megoldása ugyanis legtöbbször olyan újfajta módszerek kifejlesztésével történik, amelyek más kérdések vizsgálatára is felhasználhatók. Másfelől egy új elmélet jelentőségét az adja, ha segítségével választ kaphatunk korábban nyitott kérdésekre.

A matematikai kutatásnak azonban része egy olyan tevékenység is, amely legalább annyira fontos, mint a problémamegoldás vagy az elméletépítés, mégsem jutalmazható kitüntetésekkel - ez pedig a sejtések felállítása. Egy-egy új problémakör felvetése vagy valamely tétel általánosítási lehetőségének megsejtése, a lehetséges tételek példákon és ellenpéldákon keresztül történő tesztelése, valamint a hozzájuk elvezető kutatási programok kidolgozása gyakran több invenciót igényel, mint egy már jól megfogalmazott nyitott probléma megoldása. Az ilyen programok megálmodói sokszor évtizedekre meghatározzák egy adott terület kutatási irányát, de éppen mivel csak álmokról van szó, nem pedig konkrét eredményekről, nehéz őket ezért jutalmazni. Így például nem kapott Fields-érmet az utóbbi évtizedek legnagyobb hatású matematikusai közül Robert Langlands és Alekszandr Beilinszon, pedig jelentőségüket mi sem bizonyítja jobban, mint hogy a 2002. évi kitüntetettek, Laurent Lafforgue és Vlagyimir Voevodszkij éppen az ő programjaik megvalósításában értek el áttörést.

Néhány jutalmazott eredmény

Végül bemutatunk néhány olyan híres eredményt, amelynek szerzőjét Fields-éremmel tüntették ki. Természetesen szó sincsen arról, hogy ezek a sok fontos jutalmazott tétel között is a legfontosabbak volnának. Válogatásunk szempontja inkább az volt, hogy olyan eredmények kerüljenek terítékre a matematika különböző területeiről, amelyek elemi eszközökkel is röviden bemutathatók.

$\displaystyle \bullet$ David Hilbert 1900-ban kitűzött nevezetes 23 problémája közül a hetedik az algebrai számok témakörével foglalkozott. Egy $\alpha$ (valós vagy komplex) számot akkor mondunk algebrainak, ha létezik olyan racionális együtthatós egyváltozós polinom, amelynek $\alpha$ gyöke; például a $\displaystyle \sqrt{2}$ algebrai szám, mert gyöke az x²-2 polinomnak. A nem algebrai számokat transzcendensnek nevezzük. A XIX. századi matematika nagy vívmányai közé tartozott, amikor 1873-ban Hermite, illetve 1882-ben Lindemann kimutatta e, illetve $\displaystyle \pi$ transzcendenciáját. 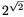Minthogy megmutatható, hogy algebrai számok összegei, szorzatai, hányadosai, sőt racionális kitevőjű hatványai is algebraiak, a következő érdekes kérdések egyike annak eldöntése, hogy például $2^{\sqrt{2}}$ transzcendens-e. Ennél Hilbert általánosabb problémát fogalmazott meg: azt sejtette, hogy ha $\displaystyle \alpha$ 0-tól és 1-től különböző algebrai szám, $\beta$ pedig irracionális algebrai szám, akkor az $\displaystyle \alpha^{\beta}$ hatvány mindig transzcendens. Hilbert e problémát nagyon nehéznek tartotta; azt jósolta, hogy (a Riemann- és a Fermat-sejtéssel ellentétben) generációjának legfiatalabbjai sem érik meg a kérdés tisztázását. Ehhez képest A. O. Gelfond már 1929-ben kimutatta $\displaystyle 2^{\sqrt{2}}$ transzcendenciáját, majd 1934-ben ugyanő és tőle függetlenül Th. Schneider megoldották az általános sejtést. Természetes alapú logaritmust véve a Gelfond-Schneider-tétel úgy is átfogalmazható, hogy nincsenek olyan $\alpha$ ₁, $\displaystyle \alpha$₂ (0-tól és 1-től különböző) algebrai számok, és olyan $\displaystyle \beta$ irracionális algebrai szám, amelyekre a log $\alpha$ ₁+$\displaystyle \beta$log $\displaystyle \alpha$₂ összeg 0. Alan Baker a Fields-érmet a következő messzemenő általánosítás bizonyításáért kapta:

Ha $\displaystyle \alpha$₁,..., $\displaystyle \alpha$_n 0-tól és 1-től különböző, $\displaystyle \beta$₁,..., $\displaystyle \beta$_n pedig nemnulla algebrai számok, amelyekre $\displaystyle \beta$₁ log $\alpha$ ₁+...+$\displaystyle \beta$_nlog $\alpha$ _n=0, akkor léteznek olyan $\gamma$ ₁,...,$\displaystyle \gamma$_n racionális számok, amelyek nem mind 0-val egyenlők, és

$\displaystyle \gamma$₁ log $\displaystyle \alpha$₁ +...+ $\gamma$ _nlog $\displaystyle \alpha$_n=0

teljesül.

E tételből levezethető például az 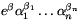$e^{\beta}\alpha_1^{\beta_1}\dots\alpha_n^{\beta_n}$ szorzatok transzcendenciája tetszőleges nemnulla $\displaystyle \alpha$₁,..., $\alpha$ _n,$\displaystyle \beta$₁,..., $\beta$ _n, $\displaystyle \beta$ algebrai számok mellett, és fontos alkalmazásai vannak a diofantikus egyenletek elméletében is.

$\displaystyle \bullet$ Erdős Pál és Turán Pál 1936-ban az alábbi érdekes problémát vetette fel:

Legyen k>2 egész szám és 0< $\delta$ <1 valós szám. Bizonyítsuk be, hogy létezik olyan (k-tól és $\delta$ -tól függő) N₀ pozitív egész, amelyre minden N $\ge$ N₀ mellett az {1, 2, 3,..., N} halmaz tetszőleges, legalább $\delta$ N elemszámú részhalmaza tartalmaz k tagú számtani sorozatot.

Magyarán, ha az {1, 2, 3,..., N} halmaz egy részhalmaza ,,nem túl ritka'', akkor elég nagy N-re biztosan tartalmaz k hosszúságú számtani sorozatot. A kérdés már k=3 mellett is nehéz, ennek megoldása volt az egyik eredmény, amelyre K. F. Roth a Fields-érmet kapta. (A másik egy alapvető tétel az ún. diofantikus approximáció területéről.) Még sokkal nehezebb azonban az általános eset, amelynek bizonyítása először Szemerédi Endrének sikerült egy rendkívül leleményes és komplikált kombinatorikai konstrukció segítségével. 1977-ben aztán Furstenberg ergodelméleti módszerek felhasználásával talált egy egyszerűbb, bár kevésbé elemi bizonyítást. Mindkét bizonyításnak hiányossága azonban, hogy nem sokat árul el az N₀ korlátról: Furstenberg csak a létezését bizonyítja, Szemerédi pedig rendkívül magas becslést ad rá, szemben Rothnak a k=3 esetben elért sokkal finomabb becsléseivel. Timothy Gowers új bizonyítása elemibb, mint Furstenbergé, kevésbé bonyolult, mint Szemerédié, és sokkal jobb korlátot ad. Ezért, és a Banach-terek elméletében elért eredményeiért kapta a Fields-érmet.

$\displaystyle \bullet$ Paul Cohen a halmazelmélet leghíresebb nyitott problémáját oldotta meg, amelyet még a tudományterületet megalapító Georg Cantor vetett fel. Cantor definiálta először a számosság fogalmát: eszerint két halmaz akkor egyenlő számosságú, ha elemeik között létesíthető kölcsönösen egyértelmű megfeleltetés. A végtelen halmazoknak mindig vannak olyan valódi részhalmazaik, amelyek velük egyenlő számosságúak: az egyik legelső (magától Cantortól származó) példa erre a racionális számok és az egész számok esete. Ugyancsak Cantor mutatta meg, hogy a valós számok számossága viszont már szigorúan nagyobb, mint a racionálisaké, és azt sejtette, hogy nincs olyan végtelen halmaz, amelynek számossága szigorúan nagyobb, mint a racionális számoké, de szigorúan kisebb, mint a valósaké. Kurt Gödel 1939-ben kimutatta, hogy e feltevés nem mond ellent a halmazelmélet általánosan elfogadott, Zermelótól és Frenkeltől származó axiómáinak. A kérdés tisztázásához azonban ez nem volt elegendő, mert csak annyit jelent, hogy létezik olyan matematikai logikai modell, amelyben a halmazelmélet Zermelo-Frenkel-féle axiómái teljesülnek, és igaz benne a Cantor-sejtés. Cohen aztán 1961-ben olyan modellt konstruált, amelyben a Zermelo-Frenkel-axiómák teljesülnek, de van benne olyan halmaz is, amely a racionális számokénál nagyobb, a valósakénál pedig kisebb számosságú. E tétel tudománytörténeti szempontból igen jelentős, hiszen az első példát szolgáltatta arra, hogy egy nevezetes nyitott kérdést egy adott axiómarendszer keretein belül nem lehet eldönteni. Másrészről Cohen a logikai modell konstrukciójához egy teljesen új, ,,forcing''-nak nevezett eljárást használt, amelynek továbbfejlesztése rendkívül gyümölcsöző későbbi kutatásoknak nyitott utat.

$\displaystyle \bullet$ A diofantikus számelmélet alapvető problémája, hogy megkeresse azokat az (x,y, z) nem azonosan 0 racionális számhármasokat, amelyek egy adott f(x, y, z) racionális együtthatós homogén polinomnak nullhelyei. Ilyen polinom például az xⁿ+yⁿ-zⁿ ,,Fermat-polinom'' vagy az y²-xz másodfokú polinom. Az f polinom meghatároz egy görbét a projektív síkon (például az y²-xz=0 egyenlet esetében ez egy kúpszelet), amelynek a keresett számhármasok a racionális koordinátájú pontjait adják. Szokásos feltevés, hogy a görbe legyen sima, azaz minden pontjához egyetlen érintőt lehessen húzni. Ha a polinom elsőfokú, a racionális pontokat könnyű megkeresni. A másodfokú eset sem sokkal nehezebb: ha van egyáltalán racionális pont, akkor végtelen sok van, és ezek egy adott pontból mind levetíthetők valamely (fix) egyenesre. A harmadfokú eset az ún. elliptikus görbék elméletéhez tartozik: itt előfordulhat, hogy nincs racionális pont, az is, hogy csak véges sok van, és az is, hogy végtelen sok; az utóbbi esetben Mordell bizonyított róluk 1930-ban egy alapvető struktúratételt. Ugyancsak ő kezdett spekulálni a magasabb fokszámú esetről is. Nyilvánvalóan ki kell itt zárnunk azon görbéket, amelyek racionális koordinátatranszformációval első, másod- vagy harmadfokúvá transzformálhatók. A többi, legalább negyedfokú görbéről viszont Mordell azt sejtette, hogy mindig csak véges sok racionális pontjuk van. Mivel túl sok numerikus példa nem támasztotta alá ezt a sejtést, általános meglepetést keltett, amikor Gerd Faltings 1983-ban bebizonyította. A bizonyítás nehéz algebrai geometriai módszereket használt, ám később Faltings (Paul Vojta és Enrico Bombieri ötleteinek továbbfejlesztésével) adott egy második, elemibb, de több számolást igénylő bizonyítást is. Mindenesetre ez a bizonyítás már kellően elemi volt ahhoz, hogy szerzője szokott szarkasztikus modorában kijelenthesse: Manapság már akárki be tudja bizonyítani a Mordell-sejtést.

$\displaystyle \bullet$ A modern algebra egyik legfontosabb fejezete a csoportok elmélete. Csoporton olyan halmazt értünk, amelyet elláttunk egy kétváltozós asszociatív művelettel (ennek leggyakoribb neve szorzás), amely két fontos tulajdonságot teljesít: a) létezik egységelem, azaz olyan e, amellyel eg=ge=g teljesül a csoport minden g elemére; b) minden g csoportelemnek létezik inverze, azaz olyan g^-1, amelyre gg^-1=g^-1g=e. Csoportot alkotnak például az egész számok az összeadásra nézve (de nem a szorzásra!), a nemnulla racionális számok a szorzásra, a sík vagy a tér egybevágóságai a kompozícióra nézve, vagy - hogy véges csoportra is mondjunk példát - a szabályos sokszögek és testek szimmetriái, ugyancsak a kompozícióra nézve. A csoportok tanulmányozásában alapvető szerepet játszanak az ún. normális részcsoportok. Egy G csoport H részhalmaza akkor normális részcsoport, ha bármely két elemével együtt azok szorzatát és inverzeit is tartalmazza, továbbá bármely h $\in$ H és g$\displaystyle \in$G mellett a ghg^-1 elemet is. 1963-ban Walter Feit és John Thompson bebizonyították Burnside egy több évtizede nyitott sejtését, amely szerint bármely véges csoport, amelynek elemszáma páratlan összetett szám, tartalmaz önmagától és az egységelemtől különböző normális részcsoportot. Ez az eredmény kiemelkedő fontosságú a véges csoportok osztályozásában, mert ,,nagyobb'' csoportok vizsgálatát ,,kisebb'' építőkövekére vezeti vissza. Thompson emellett más jelentős eredményeket is elért a véges csoportok vizsgálatában, ezért kapta ő a Fields-érmet.

$\displaystyle \bullet$ Utolsó példánk a topológia témaköréből való, és azoknak szánjuk, akik már ismerik e terület alapfogalmait. Emlékeztetünk rá, hogy d-dimenziós topologikus sokaságon olyan összefüggő topologikus teret értünk, amelyben minden pontnak van olyan nyílt környezete, amelyből létezik homeomorfizmus (mindkét irányban folytonos bijekció) a d-dimenziós euklideszi tér egy nyílt részhalmazára. A topológia egyik központi problémája a sokaságok osztályozása. Az osztályozás történhet homeomorfizmus erejéig, de legalább olyan fontos a homotópiatípus szerinti osztályozás. Szemléletesen két sokaság homotópiatípusa akkor egyezik meg, ha egymásba folytonosan átdeformálhatók. Például a körlap, sőt akármilyen konvex síkidom homotópiatípusa azonos a pontéval (mert ,,összehúzhatók''). [A precíz definíció a következő: két 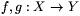$f,g:X\to Y$ folytonos leképezés homotóp (jelben: f 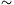$\sim$ g), ha létezik$\displaystyle h:X\times[0,1]\to Y$ folytonos leképezés, amelyre h(x,0)=f(x) és h(x,1)=g(x) minden x $\in$ X mellett. 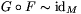Ezek után akkor lesz az M és N sokaságok homotópiatípusa azonos, ha léteznek $\displaystyle F:M\to N$ és $\displaystyle G:N\to M$ folytonos leképezések, amelyre $G\circ F\sim\mathop{\rm id}\nolimits_M$ és $\displaystyle F\circ G\sim\mathop{\rm id}\nolimits_N$.] Az általánosított Poincaré-sejtés szerint minden olyan kompakt sokaság, amelynek a homotópiatípusa azonos az S^d d-dimenziós gömbfelületével, valójában homeomorf is S^d-vel. A sejtés 2-dimenziós esetét nem nehéz igazolni, viszont a d=3 eset (Poincaré eredeti sejtése) ma is nyitott. Ezek után meglepőnek tűnhet, hogy 1982-ben Michael Freedmannek sikerült bizonyítania a d=4 esetet; mitöbb, ő valamennyi ún. egyszeresen összefüggő kompakt 4-dimenziós sokaságot osztályozni tudta. A Fields-érmesek közül Stephen Smale munkássága is a Poincaré-sejtéshez kapcsolódik: őt azért jutalmazták, mert bebizonyította a sejtést tetszőleges d>4 mellett olyan sokaságokra, amelyeken létezik differenciálható struktúra. A 3-dimenziós eset azonban továbbra is ellenáll, így nem csoda, hogy 2000-ben a Clay alapítvány felvette azon 7 millenniumi probléma sorába, amelyeknek megoldását 1 000 000 dollárral díjazza. Ha tehát a kedves olvasók valamelyike még 40 éves kora előtt megoldja ezt a 100 éve nyitott problémát, nemcsak a Fields-éremre számíthat bizton, hanem arra is, hogy dollármilliomos lesz belőle.

Szamuely Tamás
MTA Rényi Intézet
szamuely@renyi.hu

Már regisztráltál?
Új vendég vagy?