 |
Az I. 434. feladat (2017. szeptember) |
I. 434. (É) A 2016. évi nyári olimpiai játékokon az atlétika férfi kalapácsvetés döntőjének eredményeit értékeljük ki táblázatkezelő-rendszerrel.
A döntő előtt a selejtező nevezési szintje 77,00 méter volt. Ezt csak ketten dobták túl, így a döntőbe a legjobb 12 eredményű versenyző jutott. A döntő 6 dobási sorozatból állt, de a 3. sorozat után csak az addigi legjobb 8 eredményt elért versenyző folytathatta tovább. A dobás távolságát centiméter pontossággal mérik. Ha a dobás érvénytelen volt, akkor az eredmény helyén az ,,\(\displaystyle \textsf{x}\)'' karakter szerepel.
A döntőbe jutott versenyzők dobási adatait rögzítettük méterben a kalapacsforras.txt tabulátorral tagolt, UTF-8 kódolású állományban.
1. Töltsük be a kalapacsforras.txt szövegfájlt a táblázatkezelő egy munkalapjára az \(\displaystyle \textsf{A1}\)-es cellától kezdődően. Munkánkat \(\displaystyle \texttt{i434}\) néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. A \(\displaystyle \textsf{J2:J13}\) tartomány celláiban írassuk ki a versenyzők legjobb dobásainak távolságát, azaz a versenyen elért eredményüket.
3. Az \(\displaystyle \textsf{A2:A13}\) tartomány celláiban egyetlen képlettel és annak másolásával határozzuk meg a versenyzők helyezését.
4. Az első három sorozat után az addigi legjobb 8 eredményt elérő versenyző folytathatja a versenyt. Az \(\displaystyle \textsf{M3}\) cellában adjuk meg a verseny folytatásához szükséges dobástávolságot.
5. Az \(\displaystyle \textsf{M2}\) cellában a selejtező nevezési szintje szerepel. Határozzuk meg függvény segítségével, hogy a verseny összes résztvevője közül hányan teljesítették ezt.
6. Az \(\displaystyle \textsf{M5}\) cellában képlettel adjuk meg, hogy a döntő összes dobásának hány százaléka volt érvénytelen.
7. Az \(\displaystyle \textsf{M6}\) cellában határozzuk meg, hogy a 3. sorozat után még versenybe maradók hány százaléka tudott még a további dobásokkal az eredményén javítani.
8. Az \(\displaystyle \textsf{M2:M6}\) cellatartományban állítsuk be a mértékegységeket.
9. Az \(\displaystyle \textsf{A15:C22}\) tartomány celláiban függvények segítségével jelenítsük meg a végeredményt, soroljuk fel helyezési sorrendben a versenyzők nevét és országát.
10. A \(\displaystyle \textsf{D2:I13}\) cellatartományban minden versenyző legnagyobb dobását feltételes formázással, félkövér betűstílussal jelenítsük meg.
11. Az \(\displaystyle \textsf{A2:J13}\) cellatartományban az első három helyezett sorának celláiban a cellakitöltését az érem színének megfelelően feltételes formázással adjuk meg: arany RGB(255,215,0), ezüst RGB(192,192,192), bronz RGB(204,153,102).
Minta:
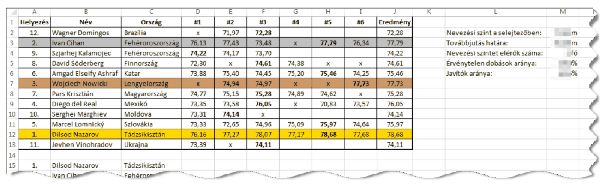
Beküldendő egy i434.zip tömörített állományban a megoldást tartalmazó munkafüzet, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott táblázatkezelő neve és verziószáma.
A munkafüzetbe importálandó adattábla: a kalapacsforras.txt.
(10 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldásokról:
Viszonylag sok megoldás érkezett, de hibátlan kevés. Az 4. feladatban többen tévesen határozták meg a továbbjutás határát. Helyesen az első három sorozat egyéni maximumai közül a 8. helyen állóé lesz.
Az 5. feladatban az M4 cellában a nevezési szint M2 cellájára kellett hivatkozni. Helyesen: =DARABTELI(J2:J13;ÖSSZEFŰZ(">=";M2))
A 6. feladatban az üres cellák a nem dobást, az x-ek a rontott dobást jelentik. Helyesen: =DARABTELI(D2:I13;"x")/DARAB2(D2:I13)
Mintamegoldás: A közölt mintamegoldás Kolláth István Tibor, a kecskeméti Bolyai János Gimnázium 11. osztályos tanulójától származik: i434.xlsx
Statisztika:
26 dolgozat érkezett. 10 pontot kapott: Bodrogai András, Csikós Patrik, Horváth 237 Lili, Kis Lázár Bence, Kolláth István Tibor, Ritter Máté, Székely Bendegúz, Ürmössy Dorottya. 9 pontot kapott: Földi Dániel, Horcsin Bálint, Hordós Adél Zita, Rittgasszer Ákos. 8 pontot kapott: 3 versenyző. 7 pontot kapott: 6 versenyző. 6 pontot kapott: 2 versenyző. 5 pontot kapott: 1 versenyző. 4 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2017. szeptemberi informatika feladatai