Az I. 656. feladat (2025. március)

I. 656. Néhány speciális egész együtthatós polinom- vagy polinomszerű függvény (hagyományos polinom tagok és abszolút értékes kifejezések keveréke) képes arra, hogy meglehetősen sok $\displaystyle x$ természetes szám helyen a függvény értéke prím legyen. Most egy speciális függvényhalmazt vizsgálunk. Ezek az $\displaystyle f(x)=x^2-x+k$ alakúak, ahol legyen $\displaystyle k<400$ természetes szám.

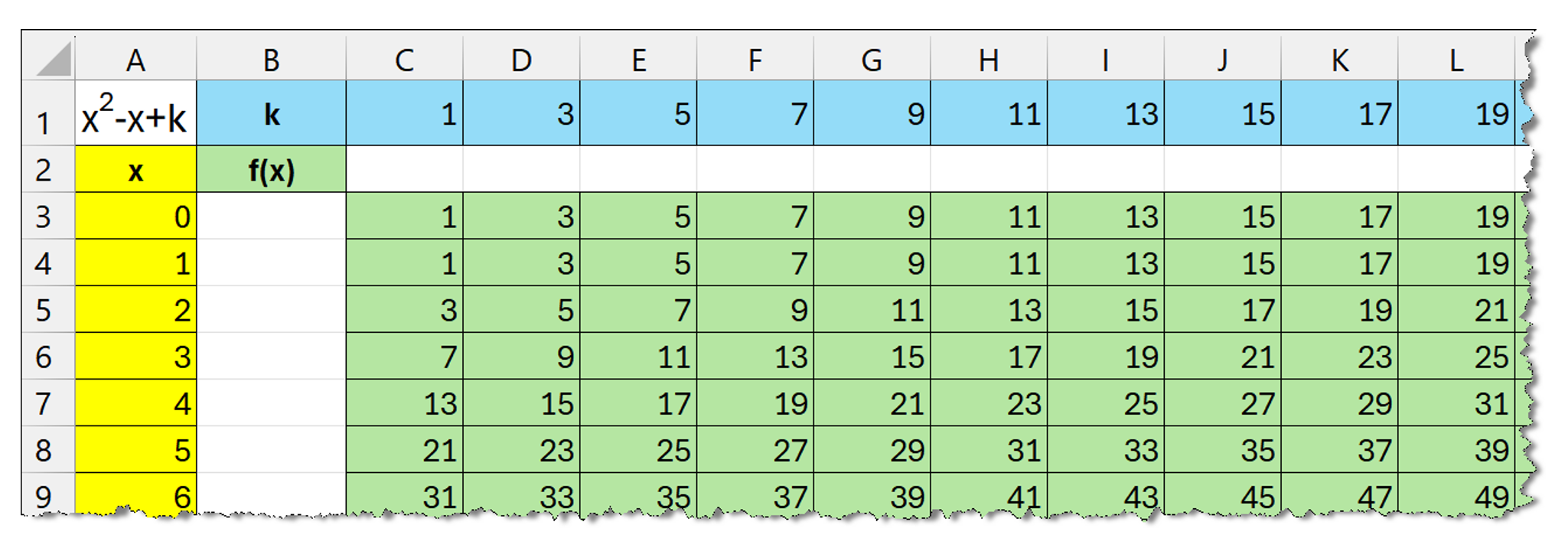
1. Nyissunk meg egy üres táblázatkezelő munkafüzetet. Készítsük el az alapadatok beviteli területét ($\displaystyle 1\leq k\leq 399$ és $\displaystyle 0\leq x\leq 399$) és az eredmény kijelzőjét a minta szerint.



2. A munkalap neve legyen adatok.
3. A cellák igazítása, szegélyezése és kitöltőszíne kövesse a mintát.
4. Számítsuk ki a C3:GT402 tartományban az adott függvény adott $\displaystyle x$-hez tartozó helyettesítési értékét.
5. Hozzunk létre prímek néven egy új munkalapot. Töltsük be erre a munkalapra az A1 cellától kezdve az UTF8 kódolású primek160000-ig.txt tartalmát.
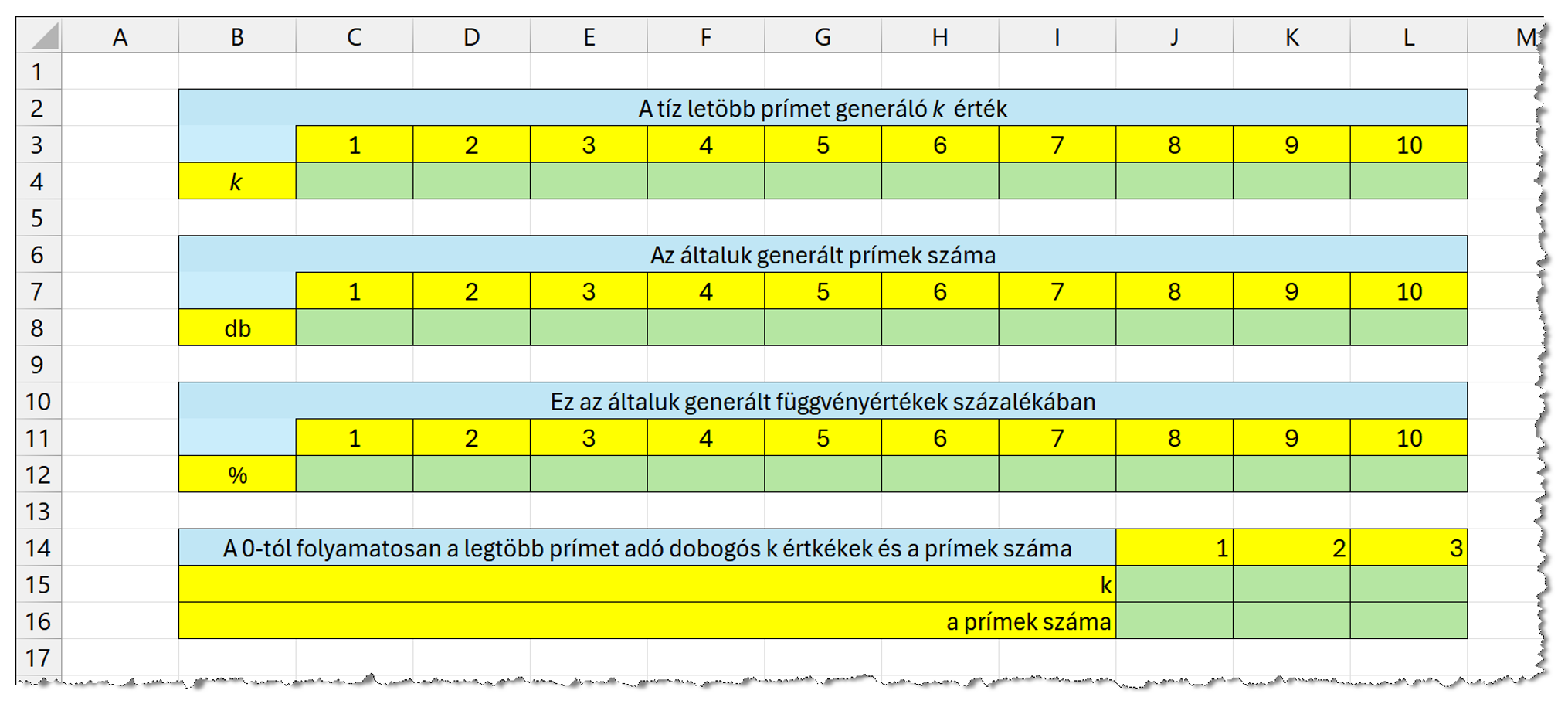
6. Hozzuk létre az eredmények munkalapot és ezen a minta szerinti táblázatot.



7. A cellák igazítása, egyesítése, szegélyezése és kitöltőszíne itt is kövesse a mintát.
8. Töltsük ki a táblázatot a megfelelő adatokkal. A százalékértékek két tizedesjeggyel jelenjenek meg.
9. A dokumentációban írjunk választ arra, hogy miért csak páratlan k értékekkel próbálkozunk.
10. A munkafüzetet mentsük primgener néven.

Segédszámításokat csak az adatok munkalapon a GU oszloptól kezdve, illetve a 403. sortól kezdve végezhetünk. A megoldásban saját függvény vagy makró nem használható.

Beküldendő egy tömörített i656.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben részletesen szerepel a 9. feladatra adott válasz és a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.

Letölthető állomány: pimek160000-ig.txt

(10 pont)

A beküldési határidő 2025. április 15-én LEJÁRT.

Rajtik Sándor Barnabás kiemelkedő megoldása primgener.xlsx

readmeexcel.txt

Statisztika:

10 dolgozat érkezett.
10 pontot kapott:	Bencze Mátyás, Gyönki Dominik, Nagy 292 Korina, Rajtik Sándor Barnabás, Szabó Imre Bence.
9 pontot kapott:	Szekeres Linda.
6 pontot kapott:	1 versenyző.
5 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. márciusi informatika feladatai