Beszámoló a 43. Nemzetközi Matematikai Diákolimpiáról

Az idei Nemzetközi Matematikai Diákolimpiát Nagy-Britanniában (közelebbről Skóciában), Glasgowban rendezték meg július 19. és 30. között 84 ország 479 diákjának részvételével. Ez mind a résztvevő országok, mind a diákok számát tekintve minden eddigi rekordot megdöntött. Az országok általában hattagú csapatokkal vettek részt, ha a csapatlétszám ennél kisebb volt, az alábbi felsorolásban az országnév után zárójelben jelzem a versenyzők számát. A résztvevők listája:

Albánia, Amerikai Egyesült Államok, Argentína, Ausztrália, Ausztria, Azerbajdzsán, Belgium, Belorusszia, Bosznia-Hercegovina, Brazília, Bulgária, Ciprus, Csehország, Dánia, Dél-Afrika, Dél-Korea, Ecuador, Észtország, Finnország, Franciaország, Fülöp-szigetek (5), Görögország, Grúzia, Guatemala (3), Hollandia, Hongkong, Horvátország, India, Indonézia, Irán, Írország, Izland, Izrael, Japán, Jugoszlávia, Kanada, Kazahsztán, Kína, Kirgizisztán (4), Kolumbia, Kuba, Kuvait (4), Lengyelország, Lettország, Litvánia, Luxemburg (2), Macao, Macedónia, Magyarország, Malajzia, Marokkó, Mexikó, Moldova, Mongólia, Nagy-Britannia, Németország, Norvégia, Olaszország, Oroszország, Örményország, Paraguay (2), Peru (5), Portugália, Puerto Rico, Románia, Spanyolország, Sri Lanka (4), Svájc, Svédország, Szingapúr, Szlovákia, Szlovénia, Tajvan, Thaiföld, Törökország, Trinidad és Tobago, Tunézia, Türkmenisztán, Új-Zéland, Ukrajna, Uruguay (1), Üzbegisztán, Venezuela (5), Vietnam.

A versenyen szokás szerint mindkét napon négy és fél óra alatt 3-3 feladatot kellett megoldani. (A feladatokat alább közöljük.) Mindegyik feladat helyes megoldásáért 7 pont járt, így egy versenyző maximális teljesítménnyel 42 pontot szerezhetett.

Az idei verseny jellegzetessége volt, hogy négy közepes/könnyű feladat mellett két igen nehéz feladat szerepelt. A 3. feladatra a 479 versenyző közül csak 14-nek, a 6. feladatra pedig csak 11-nek sikerült a maximális 7 pontot megszereznie. Így is volt három diák (két kínai és egy orosz), aki 42 pontot szerzett, mindenki másnak viszont legfeljebb 36 pontja volt. Aranyérmet 29-42 ponttal, ezüstérmet 23-28 ponttal, bronzérmet pedig 14-22 ponttal lehetett szerezni.

A magyar csapatból

Rácz Béla (Fazekas M. Főv. Gyak. Gimn., 10. o.t.) 32 ponttal aranyérmet,
Csóka Endre (Debrecen, Fazekas M. Gimn., 11. o.t.) 26 ponttal és
Csikvári Péter (Fazekas M. Főv. Gyak. Gimn., 12. o.t.) 23 ponttal ezüstérmet, míg
Kovács Erika 22 ponttal,
Harangi Viktor 21 ponttal és
Gerencsér Balázs 18 ponttal (mindhárman Fazekas M. Főv. Gyak. Gimn., 12. o.t.) bronzérmet nyert.

A csapat vezetője Pelikán József (ELTE, Algebra és Számelmélet Tanszék), helyettes vezetője Dobos Sándor (Fazekas M. Főv. Gyak. Gimn.) volt.

Az országok (nem-hivatalos) pontversenyében Kína és Oroszország kimagaslott a mezőnyből. Magyarország a (holtversenyes) 12. helyen végzett, ami a roppant erős mezőnyt figyelembe véve elfogadható eredmény.

Következzék a csapatverseny első 20 helyezettjének listája, pontszámaik feltüntetésével:

1. Kína 212, 2. Oroszország 204, 3. USA 171, 4. Bulgária 167, 5. Vietnam 166, 6. Dél-Korea 163, 7. Tajvan 161, 8. Románia 157, 9. India 156, 10. Németország 144, 11. Irán 143, 12-13. Kanada és Magyarország 142, 14-15. Belorusszia és Törökország 135, 16-17. Japán és Kazahsztán 133, 18. Izrael 130, 19. Franciaország 127, 20. Ukrajna 124.

A versenyzők felkészítésében a csapatvezetők mellett Reiman Istvánnak volt kiemelkedő szerepe, aki ezt a munkát sok-sok éve csinálja. Ezúton szeretnék neki ismét köszönetet mondani.

Az egyes versenyzők tanárai a következők voltak:

Rácz Béla:	Hraskó András, Surányi László, Pósa Lajos
Csóka Endre:	Balázs Tivadar, Pósa Lajos
Csikvári Péter, Gerencsér Balázs, Harangi Viktor és Kovács Erika:	Fazakas Tünde, Táborné Vincze Márta, Pósa Lajos

Valamennyiüknek hálás köszönet.

A verseny lebonyolítása szakmai szempontból kiemelkedően magas színvonalú volt. A versenyzők több érdekes kiránduláson is részt vehettek: eljutottak Európa egyik legszebb városába, a skóciai Edinburgh-ba és a történelmi emlékekben szintén gazdag angliai York-ba. A végére még jutott a diákoknak és tanároknak egy közös kirándulás a lapátkerekes Waverley gőzhajón, ami már csak azért sem aratott osztatlan sikert, mert mindannyian bőrig áztunk. Viszont a vendéglátók kedvességére tényleg nem lehetett panasz.

A Nemzetközi Matematikai Diákolimpiáknak van egyfajta irányító testülete, az ,,Advisory Board''. Ez öt választott képviselőből áll (elnök, titkár és három tag), továbbá a következő két év, az adott év és az előző év olimpiáját rendező ország is delegál 1-1 tagot. Ennek a testületnek az elmúlt tíz évben tagja voltam, most pedig megválasztottak az Advisory Board elnökévé.

A jövő évi diákolimpiát Japánban, Tokióban rendezik július 7. és 19. között.

Pelikán József

A 43. Nemzetközi Matematikai Diákolimpia feladatai

Első nap

1. Legyen n pozitív egész szám. Legyen T a sík azon (x,y) pontjainak halmaza, amelyekre x és y nemnegatív egész számok és x+y<n. T minden pontját pirosra vagy kékre színezzük. Ha az (x,y) pont színe piros, akkor T minden olyan (x',y') pontjának a színe is piros, amire x'\(\displaystyle \le\)x és y'\(\displaystyle \le\)y mindegyike teljesül. Nevezzük X-halmaznak az olyan halmazokat, amelyek n olyan kék pontból állnak, amelyek x-koordinátái mind különbözőek, és nevezzük Y-halmaznak az olyan halmazokat, amelyek n olyan kék pontból állnak, amelyek y-koordinátái mind különbözőek. Bizonyítsuk be, hogy az X-halmazok száma megegyezik az Y-halmazok számával.

2. Legyen BC az O középpontú \(\displaystyle \Gamma\) kör egy átmérője. Legyen A a \(\displaystyle \Gamma\) kör egy olyan pontja, amire 0^o< AOB\(\displaystyle \angle\)< 120^o. Legyen D a C-t nem tartalmazó AB ív középpontja. Az O-n keresztül DA-val párhuzamosan húzott egyenes messe az AC egyenest a J pontban. OA felezőmerőlegesének és \(\displaystyle \Gamma\)-nak metszéspontjai legyenek E és F. Bizonyítsuk be, hogy J a CEF háromszög beírt körének a középpontja.

3. Határozzuk meg az összes olyan (m,n) párt, ahol m, n egész számok, amikre m,n\(\displaystyle \ge\)3, amelyekhez létezik végtelen sok olyan a pozitív egész szám, amire

\(\displaystyle \frac{a^m+a-1}{a^n+a^2-1} \)

egész szám.

Második nap

4. Legyen n 1-nél nagyobb egész szám. n összes pozitív osztója d₁,d₂,...,d_k, ahol 1=d₁<d₂<...<d_k=n. Legyen D=d₁d₂+ d₂d₃+ ...+d_k-1d_k.

(a) Bizonyítsuk be, hogy D<n².

(b) Határozzuk meg az összes olyan n számot, amire D osztója n²-nek.

5. Határozzuk meg az összes olyan f függvényt, ami a valós számok R halmazát önmagába képezi és amire

(f(x)+f(z)) (f(y)+f(t))= f(xy-zt)+ f(xt+yz)

teljesül minden x,y,z,t\(\displaystyle \in\)R esetén.

6. Legyenek \(\displaystyle \Gamma\)₁, 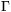₂, ..., \(\displaystyle \Gamma\)_n egységsugarú körök a síkban, ahol n\(\displaystyle \ge\)3. Jelölje a középpontjaikat rendre O₁,O₂,...,O_n. Tegyük fel, hogy nincs olyan egyenes, aminek kettőnél több körrel van közös pontja. Bizonyítsuk be, hogy

\(\displaystyle \sum_{1\le i