Matematikából kitűzött gyakorlatok és feladatok
1998. április

Általános iskolások részére javasolt példák: C. 501., C. 503., Gy. 3198., Gy. 3201.

A pontversenyben kitűzött C gyakorlatok

C. 501. Egyik reggel az iskolában a táblára fel voltak írva az egymás után következő egész számok 1-től kezdve egy bizonyos számig. A hetes az egyik számot gondosan letörölte. Az egész ügy feledésbe merült volna, ha valaki nem jegyzi meg, hogy a megmaradt számok számtani közepe 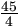volt. Próbáljuk meg kinyomozni, hogy melyik számot törölte le a hetes.

C. 502. Az x²-2bx+b²-c²=0 egyenlet gyökeit jelölje x₁ és x₂. Mutassuk meg, hogy az x²-2b(b²+3c²)x+(b²-c²)³=0 egyenlet gyökei 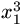és .

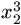C. 503. Két egyenlő szárú háromszög beírt köre az egyik esetben a szárakat az alaphoz közelebb eső harmadolópontjukban, a másik esetben az alaptól távolabb lévő harmadolópontjukban érinti. Melyik esetben fedi a beírt kör a háromszög területének nagyobb hányadát?

C. 504. Adottak a térben az A, B, C, D, E, F pontok. A pontok milyen elhelyezkedése esetén létezik olyan sík, amelytől a pontok egyenlő távolságra vannak, és amely az A, B, C ponthármast elválasztja a D, E, F pontoktól?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. május 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3198. Vannak-e olyan a, b, c, d pozitív egész számok, amelyekre ab=cd, és az a+b+c+d összeg értéke prím?

Iráni versenyfeladat

Gy. 3199. Oldjuk meg az egész számok körében az 1996x+1998y+1=xy egyenletet.

Ír versenyfeladat

Gy. 3200. Legyen H a {0, 1, 2, ..., 1998} halmaznak egy 1000 elemű részhalmaza. Bizonyítsuk be, hogy H-nak vannak olyan a, b nem feltétlenül különböző elemei, amelyekre a+b értéke 2-hatvány.

Gy. 3201. Egy 9x9-es sakktáblát lefedtünk 1x2-es dominókkal úgy, hogy valamelyik sarka üresen maradt. Bizonyítsuk be, hogy a táblán a dominókat tologatva az üres mező bármelyik sarokba ,,átvihető''. (H)

Gy. 3202. Daraboljunk fel egy n cm élű tömör kockát 1 cm élű kockákra (n természetes szám). Mely n esetén lehet a kapott kis kockákból 2n cm élű kockát összeállítani, ha megengedjük, hogy a kocka belsejében üreg is lehessen?

Gy. 3203. Egy rombusz átlóinak hossza 2a, illetve 2b. A beírt körnek az átlókkal párhuzamos érintői és a rombusz oldalai egy nyolcszöget határoznak meg. Fejezzük ki a nyolcszög területét a-val és b-vel.

Gy. 3204. Az AB és CD szakaszok párhuzamosak. A BC szakasz egy belső pontja P, az AP egyenes a CD egyenest E-ben metszi. Hogyan kell a P pontot megválasztani, hogy az APB és CPE háromszögek területének összege a lehető legkisebb legyen?

Gy. 3205. Az ABC hegyesszögű háromszög oldalaira kifelé félköröket szerkesztünk. Az A, B, C csúcsokból húzott magasságvonalak a félköröket rendre az E, F, G pontokban metszik. Bizonyítsuk be, hogy az AGBECF hatszögből egy ABC alapú gúla modellje készíthető el. (H)

Szlovák versenyfeladat

A pontversenyben kitűzött feladatok

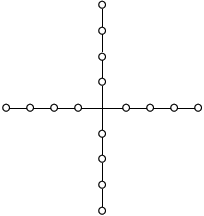
F. 3226. Az ábra köreit hány különböző módon színezhetjük ki úgy, hogy mindegyik ágon 2 sárga és 2 kék legyen? Különbözőnek csak azokat az ábrákat tekintjük, amelyek forgatással vagy tükrözéssel nem hozhatók fedésbe.

Javasolta: Bakonyi Gábor, Budapest

F. 3227. Milyen m értékek mellett osztható az x^m+y^m+z^m-(x+y+z)^m polinom az (y+z)(z+x)(x+y) polinommal?

F. 3228. Az A városból a B városba busszal lehet eljutni. A buszok félóránként indulnak, és legfeljebb 50 ember fér fel rájuk. Azok az utasok, akik nem férnek föl, a váróteremben várakoznak, aki pedig a váróterembe sem jut be, mert megtelt, az elindul gyalog B-be. Két busz indulása között 0, 25, 50 vagy 75 utas érkezhet ugyanakkora (1/4) valószínűséggel. Egy új várótermet akarnak építeni a régi helyébe, amely modulokból épül, ezért a befogadóképessége csak 25-nek többszöröse lehet. Legalább mekkorára építsék ezt az új várótermet, ha azt szeretnék, hogy 1%-nál kisebb valószínűséggel forduljon elő, hogy valakinek gyalog kell mennie?

F. 3229. Fejezzük ki a háromszög c oldalát az a és b oldalak segítségével, ha tudjuk, hogy a c oldalhoz hozzáírt kör sugara mértani közepe az a és b oldalakhoz hozzáírt körök sugarának.

Javasolta: Bodrogi Klára, Hódmezővársárhely

F. 3230. Legyen az ABC háromszög súlypontja S. A háromszög minden csúcsából bocsássunk merőlegeseket a másik két csúcshoz tartozó külső és belső szögfelezőkre. Bizonyítsuk be, hogy a kapott merőleges szakaszok négyzetének összege 6(SA²+SB²+SC²).

Javasolta: Bíró Bálint, Eger

F. 3231. A g gömb egy rögzített belső P pontján átmenő h₁, h₂ és h₃ húrjai páronként merőlegesek egymásra. A húrok által meghatározott három sík egy-egy kört metsz ki a gömbből. Mutassuk meg, hogy a három kör területének összege nem függ a húrok helyzetétől.

A pontversenyben kitűzött nehezebb feladatok

N. 171. Adottak a síkban az e₁, e₂, ..., e_n egyenesek és a P pont. A P pontot merőlegesen vetítjük az első egyenesre, a képét levetítjük a soron következő egyenesre stb. Az utolsó egyenesről ismét az elsőre vetítünk, és folytatjuk az eljárást. Bizonyítsuk be, hogy a P pont vetületei korlátos ponthalmazt alkotnak.

Javasolta: Dr. Pap Gyula, Debrecen

N. 172. Egy kártyakeverő gép egy 2n elemű paklit a következő módon tud megkeverni: (1, 2, 3, ..., 2n-1, 2n)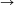(2n, 1, 2n-1, 2, ..., n+1, n). Bizonyítsuk be, hogy legfeljebb 2n keverési lépés után a kártyákat eredeti sorrendben kapjuk vissza.

Javasolta: Kovács Zoltán, Szeged

N. 173. Felbontható-e egy 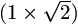-es téglalap véges sok négyzetre?

Javasolta: Pap Júlia, Debrecen

N. 174. Egy fagráf bejárásának nevezzük a következőt: egy bábu az élek mentén lépkedve eljut minden csúcshoz, és minden élen pontosan kétszer megy végig. Két bábu egyszerre járja be a fát, ha egyszerre indulnak, esetleg különböző csúcsokból, és időegységenként egyet-egyet lépnek. Két bábu akkor találkozik, ha egyszerre lépnek ugyanarra a csúcsra, vagy egyszerre tartózkodnak ugyanazon az élen. Jelöljük f(n)-nel azt a legnagyobb számot, amelyre létezik olyan n csúcsú fa, amit f(n) darab bábu egyszerre be tud járni úgy, hogy egyetlen találkozás sem történik. Bizonyítsuk be, hogy f(5k+1)=2k, ha k pozitív egész.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. május 15.