Matematikából kitűzött gyakorlatok és feladatok
1998. december
Általános iskolásoknak javasolt feladatok: C. 521, C. 524, Gy. 3240, Gy. 3238, Gy. 3242.
 |
A pontversenyben kitűzött C gyakorlatok |
C. 521. 1512 Ft-unk van 2, 5, 10, 20, 50, 100 és 200 Ft-os címletekben. (Mindegyik előfordul.) A pénz 1512-féleképpen osztható el a jobb és a bal zsebünkbe, beleértve azt a két esetet is, amikor valamelyik zsebünk üres. Hány darabot tartalmaz az összeg az egyes címletekből? (Az azonos címletű pénzeket nem különböztetjük meg.)
Javasolta: Bakonyi Gábor, Budapest
C. 522. Keressük meg az y=x2 egyenletű parabolának azokat az érintőit, amelyek 45o-os szöget zárnak be a fókuszpontból az érintési pontba húzott szakasszal.
C. 523. Egy R sugarú gömbből levágott gömbszeletet határoló gömbsüveg felszíne a gömbszeletet határoló körlap területének c-szerese (c>1). Mekkora a gömbszelet magassága?
C. 524. Az egyenlő szárú ABC háromszögben AC=BC. Adott az AB oldalon egy P pont úgy, hogy ACP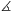 =30o, valamint a háromszögön kívül egy Q pont úgy, hogy
=30o, valamint a háromszögön kívül egy Q pont úgy, hogy
CPQ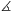 =CPA
=CPA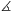 +APQ
+APQ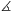 =78o.
=78o.
Az ABC és a QPB háromszög szögei fokokban kifejezve egészek. Mekkorák e két háromszög szögei?
Javasolta: Müncz Márton, Budapest
A C gyakorlatok megoldásai a következő címekre küldhetők:
KöMaL Szerkesztőség (C gyakorlatok), Budapest, Pf. 47. 1255
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)
A beküldési határidő: 1999. január 15.
 |
A pontversenyben kitűzött gyakorlatok |
Gy. 3238. Hány dobókocka esetén a legnagyobb annak a valószínűsége, hogy a kockákat egyszerre feldobva pontosan egy hatos lesz a kapott számok között?
Gy. 3239. Határozzuk meg azokat az x,y,z egész számokat, amelyekre
(x-y-1)3+(y-z-2)3+(z-x+3)3=18.
Javasolta: Kovács Béla, Szatmárnémeti
Gy. 3240. Egy 9x9-es sakktábla minden mezőjébe +1-et vagy -1-et írtunk. Első lépésként minden mezőbe beírjuk az élszomszédos mezőkben levő számok szorzatát. Ezt a lépést akárhányszor megismételhetjük. Igaz-e, hogy véges sok lépés után visszajutunk a kiindulási állapothoz?
Kínai versenyfeladat
Gy. 3241. Van-e az 1, 1, 2, 2, ..., 1998, 1998 számoknak olyan sorrendje, amelyben minden 1 n
n 1998-ra az n két előfordulása között pontosan n darab szám van? (H)
1998-ra az n két előfordulása között pontosan n darab szám van? (H)
Gy. 3242. Egy konvex négyszög belsejében található olyan pont, amelyet a csúcsokkal összekötve négy egyenlő területű háromszöget kapunk. Bizonyítsuk be, hogy ez a pont rajta van a négyszög egyik átlóján.
Gy. 3243. Osszuk fel a síkot 1000 részre a lehető legkevesebb egyenes felhasználásával. (H)
Gy. 3244. Két hasonló és azonos körüljárású háromszög megfelelő csúcsait összekötő szakaszokat megfeleztük. Bizonyítsuk be, hogy ha ezek a felezőpontok háromszöget alkotnak, akkor ez a háromszög az eredetiekhez hasonló.
Gy. 3245. Melyik az a legkisebb k természetes szám, amelyre igaz a következő állítás? ,,Ha egy tetraéder élszögei között van k darab 60o-os, akkor a tetraéder csak szabályos lehet.''
 |
A pontversenyben kitűzött feladatok |
F. 3256. Legyenek x1, x2, ..., xn pozitív valós számok, amelyek összege 1. Bizonyítsuk be, hogy ekkor:
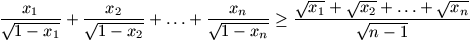 .
.
F. 3257. A [-1, 1] szakaszon értelmezett x 2x3-2x függvény grafikonjának melyik két pontja van egymástól a legtávolabb?
2x3-2x függvény grafikonjának melyik két pontja van egymástól a legtávolabb?
F. 3258. Az (an) sorozat első eleme pozitív egész szám. A sorozat további elemeire
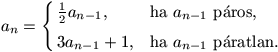
Bizonyítsuk be, hogy a sorozat elemei között mindig található 4-gyel osztható szám.
F. 3259. Egy derékszögű háromszög 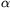 és
és 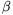 hegyesszögeire:
hegyesszögeire:
tg 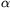 +tg
+tg 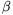 +tg 2
+tg 2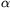 +tg 2
+tg 2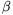 +tg 3
+tg 3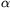 +tg 3
+tg 3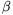 =70.
=70.
Határozzuk meg a szögeket.
Javasolta: Fitos László, Esztergom
F. 3260. A sík A1, A2, ..., An, B és C pontjairól tudjuk, hogy
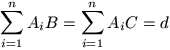 ,
,
továbbá a sík minden P pontjára igaz,hogy
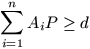 .
.
Mutassuk meg, hogy az A1, A2, ..., An pontok egy egyenesen vannak.
F. 3261. Mutassuk meg, hogy ha a tér v1, v2, v3, v4 nem egy síkban lévő vektorainak összege 0, akkor létezik olyan tetraéder, amelynek S1, S2, S3, S4 lapjai merőlegesek a vi vektorokra, és Si területének mérőszáma megegyezik vi hosszának mérőszámával.
 |
A pontversenyben kitűzött nehezebb feladatok |
N. 191. Jelölje Ln a Lucas-sorozat n-edik elemét (L0=2, L1=1, Ln+1=Ln+Ln-1), és legyen a1, a2, ... egész számokból álló olyan sorozat, amelyre tetszőleges pozitív egész n esetén
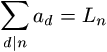
teljesül. Igazoljuk, hogy tetszőleges n pozitív egészre n|an.
N. 192. A H halmaz elemei a pozitív egész számok halmazának bizonyos részhalmazai, közülük bármely két különbözőnek a metszete véges halmaz. Következik-e ebből, hogy H megszámlálható?
Javasolta: Szabó Jácint, Győr
N. 193. Bizonyítsuk be, hogy ha n kellően nagy pozitív egész, akkor létezik olyan p polinom, amelyre
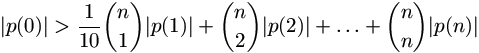 ,
,
és a foka legfeljebb 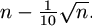 .
.
N. 194. Megadható-e véges sok pozitív egész szám: a1<a2<...<an úgy, hogy
- a belőlük készíthető, különböző tagokból álló összegek, beleértve az egytagú összegeket is, mind különbözők;
- 2)tetszőleges olyan an+1>an egészre, amelyre az a1, a2, ..., an, an+1 számokból készíthető összegek is mind különbözők, an+1>1998an teljesül?
Javasolta: Kun Gábor, Budapest
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

