A 2000. szeptemberi B-jelű matematika feladatok megoldása

Bizonyos feladatoknál csak a megoldás vázlatát, esetleg a végeredményt közöljük.

B. 3382. Bizonyítsuk be, hogy ha 17 különböző pozitív prímszám négyzetének összege négyzetszám, akkor közülük a két legnagyobb négyzetének a különbsége osztható a legkisebbel. (3 pont)

Javasolta: Gyurcsek András, Veszprém

Megoldás. Egy négyzetszám 3-mal osztva osztva 0 vagy 1 maradékot ad. Ezért 17 négyzetszám összege csak úgy lehet négyzetszám, ha van közöttük 3-mal osztható. A 17 prímszám közül az egyik a 3. A legkisebb prím ezért a 2 vagy a 3. A két legnagyobb prímszám nem osztható sem 2-vel, sem 3-mal; négyzeteik 6-tal osztva 1 maradékot adnak. Ezért a két legnagyobb prímszám négyzetének összege osztható 2-vel és 3-mal is.

B. 3383. Derékszögű háromszögben s_a és s_b a befogókhoz, s_c pedig az átfogóhoz tartozó súlyvonal. Határozzuk meg az 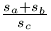kifejezés maximumát. (3 pont)

Javasolta: Besenyei Ádám, Tatabánya

Megoldás.

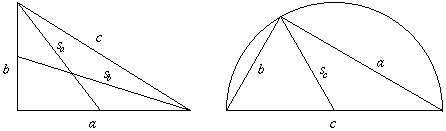
A Pitagorasz-tételből

s_a²=(a/2)²+b²,

s_b²=b²+(a/2)²,

a Thalész-tétel megfordításából pedig

s_c=c/2.

A számtani és négyzetes közép közötti egyenlőtlenség alapján

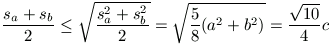
amiből

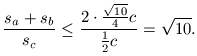
Egyenlőség akkor van, ha a=b.

B. 3384. Bizonyítsuk be, hogy ha a, b, c>0, akkor:

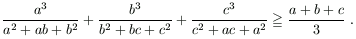(3 pont)

Javasolta: Ábrány Miklós, Beregszász

Megoldás. Bebizonyítjuk, hogy 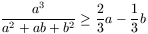, 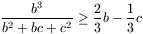és 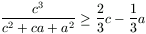. Ezek összege éppen a bizonyítandó állítás.

A betűzés ciklikus szimmetriája miatt elég az első egyenlőtlenséget bebizonyítani. Beszorzás után az egyenlőtlenség a következő alakba írható: 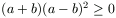, ez pedig mindig teljesül.

B. 3385. Az ABC háromszögben BC=AC+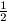AB. P az AB oldal B-hez közelebb eső negyedelőpontja. Bizonyítsuk be, hogy PAC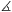=2CPA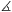. (4 pont)

Megoldás. Rajzoljunk egy C középponttú, b sugarú k kört. Messe ez AB-t D-ben, CB-t pedig E-ben.

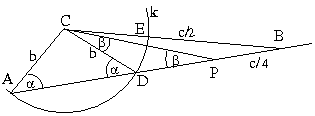
Jelölje k(B) a B pont k-ra vonatkozó hatványát. Ekkor k(B)=BE^.(BE+2b)=c/2(c/2+2b)=BD^.BA=BD^.c. Ezekből következik, hogy BD=b+c/4, így PD=BD-c/4=b és DC=b, ezért PD=DC, azaz a PDC háromszög egyenlő szárú, és így =2.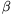

B. 3386. Egy 5x5x10-es téglatestben adott 2001 pont. Bizonyítsuk be, hogy ki tudunk közülük választani kettőt, amelyek távolsága legfeljebb 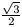. (4 pont)

Javasolta: Ábrány Miklós, Beregszász

Megoldás. Bontsuk fel a téglatestet 0.5 élű kockákra; ezek száma 5x5x10=2000. A skatulya-elv szerint van két olyan pont, amelyek ugyanabba a kockába esnek. Ezek távolsága legfeljebb akkor, mint a kocka testátlója, azaz .

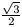Megjegyzés. A 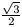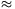0,866-nál jobb becslést (0,7) ad az A. 242. feladat.

B. 3387. Egy nem 0 p vektornak és a 2 szögű elforgatottjának az összege egyenlő a p vektor szögű elforgatottjával. Mekkora az szög? (3 pont)

Megoldás.

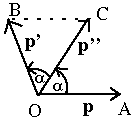
Legyen először 0^o<<180^o. Tekintsük a fenti ábrát. OA=OC=OB. Mivel a vektorösszegzés miatt az OABC négyszög paralelogramma, ezért AC=OB, tehát az OAC háromszög szabályos. Így =60^o. Tehát az elforgatás szöge lehet 60^o+k^.360^o, ahol k tetszőleges egész szám.

B. 3388. Az ABC háromszög B csúcsánál 120^o-os szög van. Ennek szögfelezője P-ben metszi az AC oldalt. A C csúcsból induló külső szögfelező Q-ban metszi az AB oldal egyenesét, a PQ szakasz pedig R-ben metszi a BC oldalt. Mekkora a PRA szög? (5 pont)

Javasolta: Katz Sándor, Bonyhád

Megoldás.

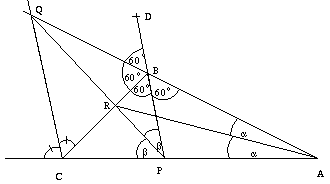
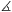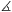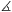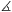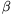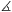Vizsgáljuk először a CPB háromszöget. QBC=180^o-120^o=60^o. Hosszabbítsuk meg PB-t egy tetszőleges D pontig. DBQ=60^o, így BQ a BCP háromszög külső szögfelezője. Külső szögfelező CQ is, így metszéspontjukat, Q-t P-vel összekötve belső szögfelezőt kapunk. Tehát CPQ=BPQ:=. Vizsgáljuk most a BPA háromszöget. Ebben BR és PR külső szögfelező, így RA belső szögfelező, és így BAR=PAR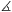:=. CPB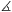 a PAB háromszög külső szöge, így 2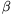=60^o+2, 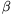=30^o+.

BPA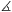=180^o-(60^o+2)=120^o-2

PRA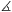=180^o-(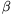+(120^o-2)+)=180^o-(30^o++120^o-2+)=30^o.

Lovrics Anna megoldása alapján

B. 3389. Legyen 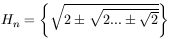, ahol a gyökjelek száma n. Hány valós eleme van az 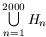halmaznak? (4 pont)

Megoldás. Legyen 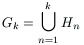. A k szerinti teljes indukcióval bebizonyítjuk, hogy a G_k halmaznak pontosan 2^k-1 különböző eleme van, és ezek mindegyike a (0,2) intervallumba esik.

Az k=1 esetben G_k=H₁-nek egyetlen eleme van, a 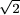, tehát az állítás igaz. Tegyük most fel, hogy az állítás igaz valamely k-ra; ebből bebizonyítjuk (k+1)-re is. Bontsuk a G_k+1 halmazt három részre:

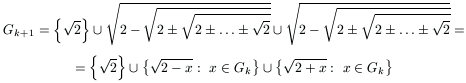
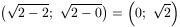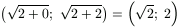A középső tagnak az indukciós feltevés miatt 2^k-1 különböző eleme van, és ezek mindegyike a intervallumba esik. A harmadik tagnak ugyanennyi eleme van a intervallumban. A két intervallum diszjunkt egmástól, tehát az elemek mind különbözők. A két intervallum részhalmaza a (0; 2) intervallumnak, tehát az összes elem (0; 2)-be esik. Az elemek száma összesen

1+(2^k-1)+(2^k-1)=2^k+1-1.

B. 3390. Egy tetraéder minden csúcsában egy-egy 5, 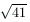és 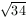hosszúságú él találkozik. Milyen hosszúak a tetraéder szemközti éleinek felezőpontjait összekötő szakaszok? (5 pont)

Megoldás. Mivel minden csúcsban különböző hosszúságú élek találkoznak, ezért a tetraéder szemközti élei egyenlő hosszúak. Így a tetraéder bennfoglaló paralelepipedonja téglatest, mert minden lapjára igaz, hogy annak átlói egyenlőek.

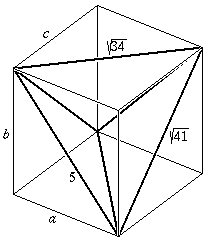
Ha a téglatest éleinek hossza a,b és c, akkor Pitagorasz tétele szerint

a²+b²=25,    b²+c²=41    és    c²+a²=34.

Ezt az egyenletrendszert megoldva kapjuk, hogy

a=3,    b=4    és    c=5.

Ezek az élhosszok éppen megegyeznek a tetraéder szemközti éleinek felezőpontjait összekötő szakaszok hosszával.