A 2002 januári A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 281. Adott a síkon véges sok pont úgy, hogy semelyik három nem esik egy egyenesre. Bizonyítsuk be, hogy a pontokat ki lehet színezni két színnel - pirossal és kékkel - úgy, hogy minden félsík, amelyik legalább három pontot tartalmaz, tartalmazzon piros és kék színű pontot is.

Megoldás. A színezésre egy algoritmust adunk. Tekintsük a pontok konvex burkát. Kezdetben színezzük a konvex burok csúcsait pirosra, a belső pontokat kékre. Ezután a következő lépést ismételgessük, ameddig csak lehet: Ha a konvex burok három szomszédos csúcsa piros, és az általuk meghatározott háromszögben nincs kék pont, akkor a három piros csúcs közül a középsőt színezzük át kékre.

A lépések sora nyilván véget ér, mert csak véges sok pontot színezünk át. A továbbiakban megmutatjuk, hogy a kapott színezés megfelelő. Nyilván elég megmutatni, hogy a pontosan három pontot tartalamzó félsíkok tartalmaznak piros és kék pontot is.

A színezésben a konvex burok bármely két szomszédos csúcsa közül legalább az egyik piros, mert a színezési eljárás során soha nem keletkezik két szomszédos kék csúcs.

Tekintsünk most egy félsíkot, amely három pontot tartalmaz. Ezek között van néhány szomszédos pont a konvex burokról (lehet, hogy csak egy), és további legfeljebb két belső pont.

Ha mindhárom pont piros, akkor ezek szomszédos pontok a konvex burokról, és az általuk meghatározott háromszögben nincs további pont. Ez azonban ellentmondás, mert a középső pontot át kellett volna színeznünk kékre.

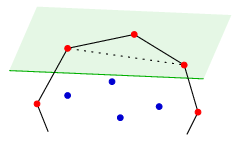
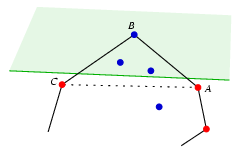
Ha mindhárom csúcs kék, akkor csak egyikük lehet a konvex burok pontja, mert a konvex burkon nincs két szomszédos kék pont. Legyen ez a pont B, a két szomszédja A és C; ezek a félsíkon kívül vannak. A B pont csak akkor lehet kék, ha az ABC háromszögben nincs kék belső pont. Ez azonban ellentmondás, mert két ilyen pont is van.

A. 282. Léteznek-e olyan f, g és h racionális törtfüggvények, amelyek minden együtthatója racionális szám, és amelyre (f(x))³+(g(x))³+(h(x))³=x?

Megoldás. Ilyen függvények léteznek. Az egyik leghíresebb példa a következő:

(1)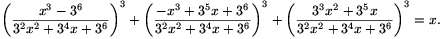

Egy lehetséges utat mutatunk, amellyel a fenti azonosságot meg lehet találni. Először olyan a(x) és b(x) polinomokat keresünk, amelyekre az a³(x)+b³(x) polinomnak van egy viszonylag magas fokú teljes köb osztója.

Legyen \(\displaystyle varrho\)=cos120^o+isin120^o az egyik harmadik egységgyök. Az a³(x)+b³(x) polinomot a komplex számok körében alakítsuk szorzattá:

(2)	a3(x)+b3(x)=(a(x)+b(x))(a(x)+.b(x))(a(x)+2.b(x)).

Az a(x) és b(x) polinomokat úgy fogjuk megválasztani, hogy a két komplex tényező - amelyek egymás konjugáltjai - teljes köb legyen, nevezetesen a(x)+^.b(x)=(x-)³ és a(x)+\(\displaystyle varrho\)^2.b(x)=(x-²)³. Ez egy lineáris egyenletrendszer az a(x) és b(x) polinomokra, aminek megoldása

a(x)=x³-3x-1,   b(x)=-3x²-3x.

A (2) jobboldalának harmadik tényezőjét teljes köbbé alakítjuk:

a(x)+b(x)=x³-3x²-6x-1=(x-1)³-9x.

Ezt és a fentieket behelyettesítve (2)-be,

(x³-3x-1)³+(-3x²-3x)³=(x-)³(x-\(\displaystyle varrho\)²)³((x-1)³-9x)=

=(x²+x+1)^3.((x-1)³-9x).

Leosztva és átrendezve:

\(\displaystyle \bigg({-x^3+3x+1\over x^2+x+1}\bigg)^3+\bigg({3x^2+3x\over x^2+x+1}\bigg)^3+(x-1)^3=9x.\)

Ebből úgy kapjuk az (1) azonosságot, hogy az x helyére x/9-et írunk.

Megjegyzés. A feladatnak sok más megoldása létezik. Mint két versenyző is felfedezte, egy további lehetséges megoldást olvashatunk Skljarszkij-Csencov-Jaglom Válogatott feladatok és tételek az elemi matematika köréből c. feladatgyűjteményében (Aritmetika és algebra, 252. feladat).

Ju. I. Manyin Kubicseszkije formi c. könyvének előszavában az (1) azonosság említése mellett algebrai geometriai eszközökkel is bebizonyítja, hogy minden racionális szám előáll három racionális szám köbösszegeként. A bemutatott eljárás kissé fáradságosan ugyan, de alkalmazható az (1)-hez hasonló azonosságok ,,gyártására'' is.

A. 283. Legyen n egész szám. Bizonyítsuk be, hogy ha az x²+xy+y²=n egyenletnek létezik racionális számokból álló megoldása, akkor létezik egész számokból álló megoldása is.

1. megoldás. A következő állítást bizonyítjuk be: Ha léteznek olyan a, b, c egész számok, amelyekre c0 és a²+ab+b²=c²n, akkor az x²+xy+y²=n egyenletnek létezik egész számokból álló megoldása. Ebből a feladat állítása következik.

Ha a=b=0, akkor n=0 és x=y=0 az egyetlen megoldás. A továbbiakban feltételezzük, hogy a és b közül legalább az egyik nem 0.

Először azt az esetet vizsgáljuk, amikor a és b relatív prímek. Ekkor relatív prímek n-hez is. Tekintsük a következő azonosságot:

=ab(x²+xy+y²)-c²xy^.n.

Az azonosságból láthatjuk, hogy ha ax-by vagy bx-ay valamelyike osztható n-nel, akkor x²+xy+y² is osztható n-nel, mert ab és n relatív prímek. A továbbiakban olyan x és y egész számok létezését bizonyítjuk, amelyekre ax-by osztható n-nel és x²+xy+y² kicsi. A bizonyítás alapötlete megegyezik az A. 274. feladat megoldásával.

Legyen H azoknak az (u,v) rácspontoknak a halmaza, amelyekre au-bv osztható n-nel. Ezek egy paralelogrammarácsot alkotnak, és egy rácsparalelogramma területe éppen akkora, ahányféle maradékot adhat egy au-bv alakú szám n-nel osztva, de mindenképpen legfeljebb n. Az origó is eleme a rácsnak.

Mint könnyen ellenőrizhető, az u²+uv+v²<2n alakú pontok egy origó középpontú ellipszis belső pontjai, amelynek területe \(\displaystyle {4\pi\over\sqrt3}n\), ami nagyobb, mint a rácsparalelogramma területének 4-szerese. Ezért a Minkowski-tétel szerint az ellipszis tartalmazza az origón kívül más pontját is a H rácsnak.

Legyen (x,y) egy origótól különböző H-beli rácspont az ellipszis belsejében. A rácspontok definíciója szerint ax-by osztható n-nel, tehát, mint láttuk, x²+xy+y² is osztható n-nel. Ugyanakkor az ellipszis definíciója miatt 0<x²+xy+y²<2n, ezért csak x²+xy+y²=n lehetséges. Ezzel az állítást bebizonyítottuk arra az esetre, ha a és b relatív prímek.

Azt az esetet, amikor a és b nem relatív prímek, visszavezetjük a relatív prím esetre. Mivel a, b és c legnagyobb közös osztójának négyzetével eloszthatjuk az egyenletet, feltételezhetjük, hogy a, b és c legnagyobb közös osztója 1. Legyen a és b legnagyobb közös osztója d. A d relatív prím c-hez és d² osztója a²+ab+b²=c²n-nek; ebből következik, hogy d² osztója n-nek is. Legyen A=a/d, B=b/d, C=c és N=n/d². Az A és B számok relatív prímek, és A²+AB+B²=C²N. Ezért a korábbiakban bizonyítottak alapján léteznek olyan X és Y egész számok, ameklyekre X²+XY+Y²=N. Az X és Y számokból az x=X^.d, y=Y^.d megoldást nyerjük az eredeti feladatra.

(Több dolgozat alapján)

2. megoldás. Ismét azt igazoljuk, hogy ha léteznek olyan a, b, c egész számok, amelyekre a vagy b nem 0 és a²+ab+b²=c²n, akkor az x²+xy+y²=n egyenletnek létezik egész számokból álló megoldása.

Felhasználjuk az Euler-egészek néhány fontos tulajdonságát. (Ezek egy összefoglalása megtalálható Kós Géza Olimpiai megjegyzések II. című cikkében.

Legyen \(\displaystyle varrho\) az első harmadik komplex egységgyök. Az a²+ab+b² szám nem más, mint a+b\(\displaystyle varrho\) normája.

Legyen a+b\(\displaystyle varrho\) prímtényezős felbontása az Euler-egészek körében p₁^.p₂^....^.p_s; a norma multiplikativitása miatt nc²=N(a+b)=N(p₁)^.N(p₂)^....^.N(p_s). Egy Euler-prím normája vagy prímszám, vagy prímszám négyzete. Ezért a prímtényezők két részre oszthatók úgy, hogy az egyik részben a normák szorzata c², a többié n. A második csoportba eső Euler-prímek szorzata tehát egy olyan Euler-egész, aminek a normája n. Ilyen tulajdonságú Euler-egész tehát létezik.