A 2002. októberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3572. Oldjuk meg az [x/2]+[x/4]=[x] egyenletet. ([x], az x egész része az x-nél nem nagyobb egészek legnagyobbika.) (3 pont)

Megoldás: Ha [x]=n, akkor [x/2]=[n/2] és [x/4]=[n/4], x tehát pontosan akkor megoldása a feladatnak, ha n=[n/2]+[n/4]. Az n számot alkalmas k egész számmal 4k, 4k+1, 4k+2 vagy 4k+3 alakban írhatjuk fel. Az első esetben egyenletünk 4k=2k+k alakba írható, ahonnan k=0, n=0. A második esetben 4k+1=2k+k, k=-1, n=-3. A harmadik esetben 4k+2=(2k+1)+k, k=-1, n=-2, a negyedik esetben pedig 4k+3=(2k+1)+k, k=-2, n=-5. A feladat megoldásai tehát azok az x számok, melyeknek egész része 0,-3,-2 vagy -5. Összefoglalva, az egyenlet megoldásainak halmaza

[-5,-4[\(\displaystyle cup\)[-3,-1[\(\displaystyle cup\)[0,1[.

B.3573. Adott az AB szakasz, annak F felezőpontja, valamint a P pont. Szerkesszünk P-n át AB-vel párhuzamos egyenest egyetlen vonalzó segítségével. (4 pont)

Megoldás: Vegyünk fel az AP szakasz P-n túli meghosszabbításán egy D pontot. Szerkesszük meg ezután a PB és DF egyenesek M metszéspontját, majd a DB és AM egyenesek C metszéspontját. Képzeljük el az AB-vel P-n keresztül húzott párhuzamos DB egyenessel alkotott C' metszéspontját. Állítjuk, hogy C=C', következésképp a PC egyenes párhuzamos az AB egyenessel.

Ennek igazolásához tekintsük a PB és AC' szakaszok M' metszéspontját. Ismert (lásd pl. Geometriai feladatok gyűjteménye I., 1246. feladat), hogy a DM' egyenes felezi az ABC'P trapéz alapjait, vagyis DM' átmegy F-en. Ez viszont azt jelenti, hogy M=M', tehát C=C', azaz PC párhuzamos AB-vel.

B.3574. A k₁ kör a P pontban belülről érinti a k₂ kört. A nagyobbik kör AB húrja a kisebbik kört a C pontban érinti, AP és BP pedig a D és az E pontban metszi a kisebbik kört. Tudjuk, hogy AB=84, PD=11, végül PE=10. Mekkora az AC hossza? (4 pont)

Megoldás. Mivel a két kör P-nél levő érintője közös, PDE\(\displaystyle mangle\)=PAB\(\displaystyle mangle\), hiszen a megfelelő körökben ahhoz az ívhez tartozó kerületi szögek, amelyhez a P-nél keletkező érintőszárú kerületi szög is tartozik (l. ábra).

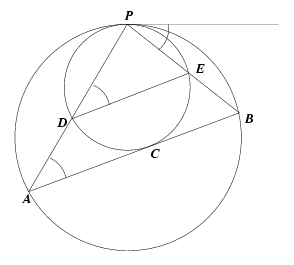
Így AP:BP=DP:EP=11:10, ezért a szelőtétel miatt

\(\displaystyle AC^2:BC^2={AP(AP-DP)\over{BP(BP-EP)}}=11^2:10^2,\)

azaz \(\displaystyle BC={10\over{11}}AC\). Innen \(\displaystyle 84=AB=AC+BC={21\over{11}}AC\), tehát \(\displaystyle AC={11\over{21}}\cdot84=44\).

B.3575. Jelölje X azoknak a pozitív egészeknek a halmazát, amelyek tízes számrendszerbeli alakjában előfordulnak különböző számjegyek. Ha nX, akkor jelöljük A_n-nel azoknak a számoknak a halmazát, amelyeket az n jegyeinek az átrendezésével kapunk, d_n-nel pedig az A_n elemeinek a legnagyobb közös osztóját. Mi a d_n legnagyobb értéke? (4 pont)

Megoldás. Először is a feladat pontatlansága, hogy nem derül ki, hogy a 10ⁿ alakú számok mind különböző halmazhoz tartoznak-e. Ezek ugyanis olyan számok, amelyek egy darab 1-esből és 0-kból állnak, így különböző számjegyeik vannak, de ha nem engedjük meg a 0-val kezdődő számokat, akkor 1-elemű halmazt alkotnak, amelyekben d_n=10ⁿ, ilyen d_n-eknek azonban nincs maximuma. Ezért feltételezzük, hogy az átrendezés során megengedjük, hogy 0-val kezdődjenek számok. (Ekkor viszont nem nyilvánvaló, hogy pl. a 17 és a 017, azaz pl. a 170 ugyanabban a halmazban vannak. Ellenkező esetben minden szám több halmazban is benne lenne, ugyan a feladat szövege ezt nem zárja ki, és a megoldást sem befolyásolja.)

Minden halmazban van két olyan szám, amelyek csak a két legkisebb helyiértéken térnek el, mert az eredeti szám minden átrendezése szerepel a halmazban, és nem ugyanaz az összes számjegy. Két ilyen szám különbsége csak 9, 18, 27, 36, 45, 54, 63, 72, 81 lehet. (Nyilván legfeljebb kétjegyű, nyilván 9-cel osztható és nyilván nem lehet 90 vagy 99.)

Van olyan n, amely 81-gyel osztható, és minden átrendezése is osztható 81-gyel. Azt kell csak elérni, hogy n 9-cel osztva még mindig osztható legyen 9-cel. Ha n 9 darab 9-esből és 0-kból áll, akkor teljesíti ezt a feltételt.

B.3576. A 0, 1, 2 számjegyekből véletlen sorozatot készítünk. Milyen hosszú sorozatok esetén lesz legalább 61% annak a valószínűsége, hogy a sorozatban mindhárom számjegy előfordul? (4 pont)

Javasolta: Fried Ervin, Budapest

Megoldás. Az n hosszúságú, egyetlen számjegyet használó sorozatok száma 3, a pontosan kétféle számjegyet tartalmazóké pedig 3(2ⁿ-2); így

\(\displaystyle p_n={3+3(2^n-2)\over{3^n}}={2^n-1\over{3^{n-1}}}\)

annak a valószínűsége, hogy egy n hosszúságú sorozatban valamelyik számjegy nem fordul elő. Könnyen belátható, hogy p_n monoton fogyó. Mivel

\(\displaystyle p_4={5\over{9}\){39\over{100}}>{31\over{81}}=p_5\,,">

a feladat követelménye a legalább 5 hosszúságú sorozatokra teljesül.

B.3577. Oldjuk meg a sin 3x + 3 cos x = 2 sin 2x (sin x + cos x) egyenletet. (4 pont)

Javasolta: Mosóczi András, Budapest

Megoldás: Az a=cosx és b=sinx jelöléseket bevezetve sin2x=2ab és

sin3x=sin2xcosx+sinxcos2x=2a²b+b(a²-b²)=3a²b-b³.

Így az egyenlet

3a²b-b³+3a=4a²b+4ab²

alakba írható, ahonnan az a²+b²=1 trigonometrikus Pithagorasz-tételt is felhasználva

3a=b(a²+b²)+4ab²=b+4a(1-a²)

adódik. Ezért b=a(4a²-1), amit négyzetre emelve az A=a² változó bevezetésével az 1-A=A(4A-1)² egyenletre jutunk. Ezt rendezve kapjuk, hogy

16A³-8A²+2A-1=(2A-1)(8A²+1)=0,

mely egyenlet egyetlen valós megoldása A=1/2. Innen \(\displaystyle b=a(4A-1)=a=\pm1/\sqrt{2}\), ahonnan x=\(\displaystyle pi\)/4+k\(\displaystyle pi\) adódik, ahol k tetszőleges egész szám. Könnyen ellenőrizhető, hogy ezek a szögek valóban kielégítik az egyenletet.

B.3578. Az ábrán látható kocka ABCD lapjának középpontja M. Keressük meg az AB és az EM egyenesen a P illetve a Q pontokat úgy, hogy a PQ távolság egyenlő legyen az AB és az EM egyenesek távolságával.

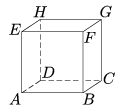
(3 pont)

Megoldás: Az AD él felezőpontját N-nel jelölve látható, hogy az AB egyenes párhuzamos az E,M és N pontokra illeszkedő S síkkal. Az AB egyenes vetülete az S síkra egy olyan e egyenes, mely AB-vel párhuzamos, és áthalad az A pont EN egyenesre eső A' vetületén, hiszen az AEN sík merőleges az S síkra és az AB egyenesre is. Az AB él hosszát 2 egységnyinek tekintve AN=1 és a Pithagorasz-tétel alapján \(\displaystyle EN=\sqrt{5}\). Az AEN és A'AN hasonló derékszögű háromszögekből tehát \(\displaystyle A'N=1/\sqrt{5}=EN/5\). Mivel a Q pont éppen az e egyenes EM egyenessel alkotott metszéspontja, az ENM és EA'Q derékszögű háromszögek hasonlóságából A'Q=(4/5)NM=4/5 és \(\displaystyle MQ=EM/5=\sqrt{6}/5\). Mivel pedig a P pont vetülete az S síkra (és egyben az e egyenesre is) Q, AP=A'Q=4/5. A P pont tehát az a pont, amely az AB szakaszt 2:3 arányban osztja, Q pedig az ME szakaszt 1:4 arányban osztó pont.

B.3579. Oldjuk meg az alábbi egyenletet:

\(\displaystyle x=\sqrt{-3+4\sqrt{-3+4\sqrt{-3+4x}}}.\)

(5 pont)

Megoldás: Az \(\displaystyle f(x)=\sqrt{4x-3}\) függvény bevezetésével az egyenlet f(f(f(x)))=x alakba írható. Oldjuk meg először az f(x)=x egyenletet: \(\displaystyle \sqrt{4x-3}=x\), x²=4x-3, melynek megoldásai x₁=1 és x₂=3, melyek nyilván az f(f(f(x)))=x egyenletet is kielégítik. Továbbá 1<x²<4x-3<9 ha 1<x<3, x²>4x-3>9, ha x>3, és 1>x²>4x-3\(\displaystyle ge\)0, ha 1>x\(\displaystyle ge\)3/4. Ha x<3/4, akkor f(x) nincs értelmezve.

Megállapíthatjuk tehát, hogy ha 1<x<3, akkor 1<x<f(x)<3, ha x>3 akkor x>f(x)>3, és ha x<1, akkor vagy f(x)<x<1, vagy pedig f(x) nincs értelmezve. Ezért 1<x<3 esetén f(f(f(x)))>x, x>3 esetén f(f(f(x)))<x, x<1 esetén pedig vagy f(f(f(x)))<x, vagy f(f(f(x))) nincs értelmezve. Az egyenletnek tehát két megoldása van: x=1 és x=3.

B.3580. Tekintsük azokat a tompaszögű háromszögeket, amelyek tompaszöge az egyik hegyesszögük kétszerese, és oldalaiknak hossza egész szám. Melyiküknek a legkisebb a kerülete? (4 pont)

Megoldás: Jelölje a háromszög szögeit \(\displaystyle alpha\),\(\displaystyle beta\),2\(\displaystyle beta\), a velük szemben lévő oldalakat pedig rendre a,b,c. Mivel 2\(\displaystyle beta\)>\(\displaystyle pi\)/2, \(\displaystyle beta\)>\(\displaystyle pi\)/4, kapjuk hogy \(\displaystyle alpha\)<\(\displaystyle pi\)/4 és a<b<c. A cos2\(\displaystyle beta\)=2cos²\(\displaystyle beta\)-1 azonosságból a koszinusz-tétel segítségével felírhatjuk, hogy

\(\displaystyle {a^2+b^2-c^2\over2ab}=2\Bigl({a^2+c^2-b^2\over2ac}\Bigr)^2-1,\)

ahonnan átrendezés és (a+b)-vel történő egyszerűsítés után a

c⁴-(a²-ab+2b²)c²+b(a-b)²(a+b)=0

egyenlőségre jutunk. Ez c²-re nézve másodfokú egyenlet, melynek diszkriminánsára rövid számolás után a²(3b-a)² adódik. Innen c² értékére két lehetőségünk van: a²-2ab+b² és b²+ab. Az első esetben c=b-a lenne, ami nem lehetséges, tehát c²=b(a+b).

Innen leolvasható, hogy ha a-nak és b-nek lenne közös osztója, akkor az c-nek is osztója lenne, és ekkor a háromszöget megfelelő arányban kicsinyítve egy hozzá hasonló, kisebb kerületű megoldást kapnank. Ezért a és b relatív prímek. Így b és a+b is relatív prímek, tehát szükségképpen négyzetszámok: b=d² és a+b=a+d²=e², alkalmas d és e pozitív egészekkel, melyekre a<d² is kell, hogy teljesüljön, vagyis d²<e²<2d². Ezért a legkisebb szóba jövő értékek d=3 és e=4, ahonnan a=7, b=9 és c=12 adódik. Mivel ezek a számok valóban egy háromszög oldalai, melyekre az először felírt egyenlőség teljesül, a koszinusz függvény [0,\(\displaystyle pi\)] intervallumban való szigorú monotonitása miatt ebben a háromszögben a c-vel szemben lévő szög, mely tompaszög, hiszen koszinuszára -1/9 adódik, valóban a b-vel szemben lévő szög kétszerese. Ez tehát a legkisebb kerületű ilyen háromszög, hiszen ha d és e értékét növeljük, akkor a,b,c értéke is növekszik. A keresett háromszög oldalai tehát 7,9 és 12, kerülete pedig 28.

B.3581. Mennyi az

f(x)=|1001+1000x+999x²+...+2x⁹⁹⁹+x¹⁰⁰⁰|

függvény legkisebb értéke? (5 pont)

Megoldás. A feladat általánosabban, 1001 helyett tetszőleges 2n+1 páratlan számra is megoldható.

f(x)=|(2n+1)+(2n)x+(2n-1)x²+...+2x^2n-1+x²ⁿ|

Jelölje g(x) a (2n+1)+2nx+2n-1x²+...+2x^2n-1+x²ⁿ polinomot. Ez a polinom a nemnegatív számokon szigorúan monoton nő. Keressük meg g(x) legkisebb értékét. Ha ez negatív, akkor g(x) -- polinom, ezért folytonos lévén -- valahol 0, hiszen pozitív x-re pozitív. Ekkor f(x) legkisebb értéke 0 lenne. g(x) legkisebb értékét a negatív x-ek körében keressük: x<0. g(x)^.(x-1)²=x²ⁿ⁺²-(2n+2)x+2n+1

. Eszerint ha x<0, akkor

\(\displaystyle \displaylines{g(x)={x^{2n+2}-(2n+2)x+2n+1\over(x-1)^2}.\cr g'(x)={(x-1)^2\left[(2n+2)x^{2n+1}-2n-2\right]-2(x-1)\left[x^{2n+2}-(2n+2)x+2n+1\right]\over(x-1)^4}.\cr}\)

g'(-1)=0. Tehát g'(x)=(x+1)h(x). Belátjuk, hogy minden más x-re h(x)>0. (Vagyis most x\(\displaystyle ne\)-1.)

\(\displaystyle \displaylines{h(x)={g'(x)\over(x+1)}=\hfill\cr={2\over(x-1)^3(x+1)}\cdot{(x-1)\left[(n+1)x^{2n+1}-n-1\right]-\left[x^{2n+2}-(2n+2)x+2n+1\right]}=\cr={2\over(x-1)^3(x+1)}\cdot\left[nx^{2n+2}-(n+1)x^{2n+1}+(n+1)x-n\right]=\cr={2\over(x-1)^3(x+1)}\cdot\left[n\cdot(x^{2n+2}-1)-(n+1)x\cdot(x^{2n}-1)\right].\cr}\)

x<-1 esetén a tört pozitív, a zárójelben szereplő kisebbítendő pozitív, a kivonandó negatív. -1<x<0 esetén pedig a tört negatív, a kisebbítendő negatív, a kivonandó pozitív. Ebből következik, hogy h(x)>0, ha x<0, x\(\displaystyle ne\)-1. f a minimumát (-1)-ben veszi fel, és az f(-1)=n+1.