A 2002 decemberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 305. Igazoljuk, hogy tetszőleges n pozitív egészre

$\displaystyle \sum_{\textstyle{k_1,\dots,k_n\geq0\atop k_1+2k_2+\dots+nk_n=n}} \frac{(k_1+k_2+\dots+k_n)!}{k_1!\cdot\ldots\cdot k_n!}=2^{n-1}.$

Megoldás. Az egyenlet mindkét oldalának ugyanaz a kombinatorikai jelentése van: ennyiféleképpen lehet egy 1xn-es rácstéglalapot kisebb rácstéglalapokra bontani. (Megengedjük azt is, hogy a felbontás csupán egyetlen darabból álljon.)

Először csoportosítsuk a felbontásokat aszerint, hogy az egyes méretű darabokból hányat tartalmaznak. Az olyan felbontások száma, amik k₁ darab 1x1-es, k₂ darab 1x2-es, ..., k_n darab 1xn-es téglalapból állnak, annyi, ahányféleképpen ezeket a téglalapokat sorba állíthatjuk. A sorba állítások száma az ismétléses kombinációk számát megadó képlet szerint $\displaystyle {(k_1+k_2+\dots+k_n)!\over k_1!\cdot\dots\cdot k_n!}$. A darabok méretének összege k₁+2k₂+...+nk_n, ami csak n lehet. Ezért a baloldal az összes lehetséges felosztást számolja össze.

A felbontásokat úgy is definiálhatjuk, hogy megmondjuk, hogy a keresztben haladó n-1 rácsegyenes közül melyek mentén vágjuk el a téglalapot. Ezért a felbontások száma az (n-1)-elemű rácsegyenes-halmaz részhalmazainak száma, azaz 2^n-1.

A. 306. Az ABC háromszög magasságpontja M, beírt köre az AC és BC oldalakat a P, illetve Q pontokban érinti, középpontja O. Bizonyítsuk be, hogy ha M a PQ egyenesre esik, akkor az MO egyenes átmegy az AB oldal felezőpontján.

Megoldás (Richter Péter megoldása). Legyen az OP sugár és az AM magasság metszéspontja U, az OQ sugár és a BM magasságvonal metszéspontja pedig V. Az ACB$\displaystyle \angle$=$\displaystyle \gamma$ jelöléssel PAM$\displaystyle \angle$=QBM=90^o-$\displaystyle \gamma$, $\displaystyle UPM\angle=UMP\angle=VMQ\angle=VQM\angle={\gamma\over2}$. Ezekből következik, hogy az APMU és BQMV pontnégyesek hasonlóak.

A két pontnégyes hasonlóságából MU:MA=MV:MB, és a párhuzamos szelők tételének megfordítása alapján az UV szakasz párhuzamos az AB szakasszal. Az OM egyenes az OVMU paralelogramma egyik átlója, ami felezi a másik, UV átlót. Mint láttuk, az UV átló párhuzamos az AB oldallal, ezért az OM egyenes az AB oldalt is felezi.

A. 307. Jelöljük a_n-nel az (x²+x+1)ⁿ polinomban az xⁿ együtthatóját. Igazoljuk, hogy tetszőleges p>3 prímszám esetén a_p1 (mod p²).

Megoldás. Legyen ₁ és $\displaystyle \varepsilon$₂ az x²+x+1 polinom két komplex gyöke; ezek nem mások, mint az 1-től különböző harmadik egységgyökök. A polinom gyöktényezős alakja (x-$\displaystyle \varepsilon$₁)(x-₂), ezért a binomiális tétel alapján

(x²+x+1)^p=(x-₁)^p(x-₂)^p=

$\displaystyle =\left(\sum_{k=0}^p(-1)^k{p\choose k}\varepsilon_1^kx^{p-k}\right) \left(\sum_{k=0}^p(-1)^k{p\choose k}\varepsilon_2^kx^{p-k}\right).$

A polinomban az x^p együtthatója:

$\displaystyle a_p=\sum_{k=0}^p (-1)^k{p\choose k}\varepsilon_1^k\cdot(-1)^{p-k}{p\choose p-k}\varepsilon_2^{p-k}= -\sum_{k=0}^{(p-1)/2}{p\choose k}^2(\varepsilon_1^{p-2k}+\varepsilon_2^{p-2k})=$

$\displaystyle =-(\varepsilon_1^p+\varepsilon_2^p)-\sum_{k=1}^{(p-1)/2}{p\choose k}^2(\varepsilon_1^{p-2k}+\varepsilon_2^{p-2k})$

Tetszőleges u egész számra az ₁^u+₂^u=2, ha u osztható 3-mal, és $\displaystyle \varepsilon$₁^u+₂^u=-1, ha u nem osztható 3-mal. Mivel p>3 és ezáltal p nem osztható 3-mal, $\displaystyle \varepsilon$₁^p+₂^p=-1. A 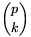binomiális együttható pedig 0<k<p esetén mindig osztható p-vel. Ezért

a_p-(₁^p+₂^p) = 1 (mod p²).