 |
A 2005. februári K-jelű matematika gyakorlatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
K. 31. Az ábrán látható hatszög minden belső szöge 120o-os. Bizonyítsuk be, hogy
AB + FA = CD + DE.
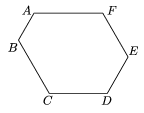
Megoldás:
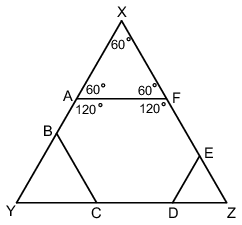
Ha a hatszög oldalait az ábrán látható módon meghosszabbítjuk, egy szabályos háromszöget kapunk, amelyből a hatszög szintén szabályos háromszögeket vág le. Tehát FA = AX és DE = DZ, ahonnan YX = YB + BA + FA és YZ = YC + CD + DE. Mivel YX = YZ és YB = YC, az előző két egyenlőségből következik, hogy BA + FA = CD + DE.
K. 32. Egy könyvtárban a következő módon választ 3 gyerek 5 féle könyv közül: az 5 féle könyv mindegyikéből egy-egy példány van egymás mellé kitéve egy asztalra, a gyerekek pedig arra a könyvre teszik az olvasójegyüket, amelyiket ki szeretnék kölcsönözni (egyféle könyvet többen is kölcsönözhetnek, akár mind a hárman, ilyenkor több olvasójegy kerül ugyanazon könyvre, ám egy gyerek csak egy könyvet kölcsönözhet). Két olvasójegy-elrendezés különbözőnek számít, ha legalább egy gyerek nem ugyanazt a könyvet jelölte meg a két elrendezésben. Hány lehetőségük van összesen az olvasójegyek elhelyezésére?
1. Megoldás: Egy-egy gyerek 5 könyv közül választhat. A választásuk független egymástól, így hárman összesen 5.5.5=125-féleképpen választhatnak.
2. Megoldás: I. eset: Mindhárman ugyanazt a könyvet választják. Ez ötféleképpen történhet. II. eset: Ketten egy könyvet, a harmadik egy másik könyvet választ. Válasszuk ki a két megjelölt könyvet! Ezt \(\displaystyle {5\cdot4\over2}=10\)-féleképpen tehetjük meg. Bármely két kiválasztott könyv esetén a gyerekek jelölése hatféle lehet: háromféle lehet az a gyerek, aki egyedül jelölte ki az egyik könyvet, és az általa megjelölt könyv is kétféle lehet. Ez tehát összesen 60-féle lehetőséget jelent. III. eset: Mindenki más-más könyvet választ. Ebben az esetben a meg nem jelölt könyveket, ezzel együtt a megjelölt könyveket is \(\displaystyle {5\cdot4\over2}=10\)-féleképpen választhatjuk ki, és a gyerekek a kiválasztott könyveket 6-féle sorrendben jelölhetik meg. Ez tehát újabb 60 lehetőség. Több pedig nincs, tehát összesen 125 lehetőség van a könyvek megjelölésére.
K. 33. Balázsnak van 11 darab műanyag hengere. Ha magasságuk szerint sorba rakja ezeket (a ,,talpukra'' állítva), akkor mindegyik 2 cm-rel nagyobb, mint az azt megelőző. A sorban a legutolsó henger éppen akkora, mint a középső és annak egyik szomszédja egymásra téve. Milyen magas oszlopot lehet építeni a 11 hengert egymásra téve?
Megoldás: A középső henger a 6. henger, ennél 10 cm-rel magasabb a 11. henger. Tehát a 6. henger szomszédja, az 5. vagy a 7. henger 10 cm magas. A 7. henger az első hengernél 12 cm-rel magasabb, ezért nem lehet 10 cm magas. Tehát az 5. henger 10 cm, és így az első henger 2 cm magas. A hengerek magassága sorban 2, 4, 6, ..., 22 cm, ezek összege pl. a Gauss-módszerrel kiszámítva 132 cm. Tehát az építhető oszlop magassága 132 cm.
K. 34. Oldjuk meg a következő egyenletet:
(x2-4)2 (x+3)2+ (x+2)2(x-9)2=0.
Megoldás: Két négyzetszám szorzata mindig nemnegatív, ezért a bal oldal csak akkor lehet 0, ha külön-külön teljesül az (x2-4)2(x+3)2=0 és az (x+2)2(x-9)2=0 egyenlőség. Az első egyenlőség x = 2; -2; -3 esetén áll fenn, a második egyenlőség pedig x = -2; 9 esetén áll fenn. Mindkettő akkor teljesül, ha x = -2, tehát ez az eredeti egyenlet egyetlen megoldása.
K. 35. Tudjuk, hogy a háromszög súlyvonalai felezik a területét, valamint, hogy egy ponton, a súlyponton haladnak át. Igaz-e, hogy azok a területfelező egyenesek, amelyek párhuzamosak a háromszög valamelyik oldalával, áthaladnak a háromszög súlypontján?
Megoldás: Nem igaz. A súlyponton átmenő, valamelyik oldallal párhuzamos egyenes olyan háromszöget vág le az eredeti háromszögből, melynek egyik oldala és magassága az eredeti háromszög megfelelő oldalának és magasságának 2/3 része, tehát területe az eredeti háromszög területének 4/9 része, azaz kevesebb, mint a fele. Tehát ez az egyenes nem felezi a területet, így az ilyen irányú területfelező egyenes nem mehet át a súlyponton.
K. 36. Hány olyan, legalább kétjegyű egész szám van, és melyek ezek, melyekre teljesül, hogy 6 milliónál kisebbek, és az őket megelőző, valamint az őket követő egész szám is palindrom? (Palindrom számnak azokat az egész számokat nevezzük, melyek számjegyeit fordított sorrendben írva az eredeti számot kapjuk.)
Megoldás: Olyan szám, amilyet keresünk, nem végződhet 2, 3, 4, ..., 8-ra. Ugyanis ebben az esetben ha 1-et levonunk belőle, illetve hozzáadunk, akkor a kapott számoknak csak az utolsó jegye fog eltérni, ezért nem lehet mindkettő palindrom. 1-re vagy 9-re sem végződhet, mert akkor szomszédai között az egyik 0-ra végződne, de ez nem lehetne palindrom. Tehát a keresett számok csak 0-ra végződhetnek. Ha viszont 0-ra végződik, akkor a rákövetkező szám (aminek palindromnak kell lennie) utolsó számjegye 1, tehát első számjegye is 1; az őt megelőző szám (aminek szintén palindromnak kell lennie) utolsó számjegye 9, tehát első számjegye is 9. Ez viszont csak úgy következhet be, ha a 0-ra végződő szám 10 valamelyik hatványa. Tehát a keresett számok: 10, 100, 1000, 10000, 100000, 1000000.

