Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:
VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek
5. rész
1. rész 2. rész 3 rész 4. rész 5. rész 6. rész 7. rész
46.
Tételezzük fel, hogy egy gyermek születésekor ugyanakkora a valószínűsége annak, hogy az újszülött fiú vagy lány. Tudjuk, hogy egy háromgyermekes családban van leány. Mennyi annak a valószínűsége, hogy valamelyik testvére fiú?
Megoldás:
Jelöljön L egy lányt, F egy fiút! LLL, LLF, LFL, FLL, LFF, FLF, FFL, FFF lehet a gyerekek neme a háromgyerekes
családokban. Összesen 23 eset fordulhat elő.
P(A=legalább az egyik gyermek lány)= 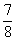
P(A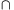 B=lány és fiú is van a gyerekek között)=
B=lány és fiú is van a gyerekek között)= 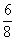
P(van fiú is a családban, ha a három gyerek egyike lány) = 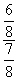 =
= 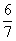 , ami körülbelül 85,7%.
, ami körülbelül 85,7%.
Tulajdonképpen a feltételes valószínűséget írtunk fel: P(B|A)= 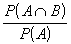
Általában, ha egy n gyermekes családban van lány, akkor 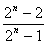 a valószínűsége, hogy van fiú is.
a valószínűsége, hogy van fiú is.
Feltételes valószínűség nélkül is kiszámíthatjuk a keresett értéket:
a lányos esetek száma 7, a lányos-fiús esetek száma 6. P= 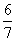 .
.
47.
A metróra váró utasok közül tizenkilencen úgy helyezkednek el, hogy a szerelvény első kocsijába szállhassanak majd, de annak egyforma az esélye, hogy a kocsi négy ajtaja közül melyiket veszik igénybe.
- Mennyi annak a valószínűsége, hogy mindannyian a második ajtón lépnek be a kocsiba?
- Számítsuk ki annak a valószínűségét, hogy az első és a negyedik ajtót is hét-hét utas, a harmadik ajtót egy utas, a második ajtót a többi utas veszi igénybe a beszálláskor!
Megoldás:
Az 19 utas egymástól függetlenül a négy ajtó közül bármelyiket igénybe veheti, az összes lehetőség 419.
- Kedvező eset csak 1 van.
P(A=19 utas a második ajtónál)=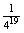 P(A)
P(A) 3,64 × 10-12.
3,64 × 10-12.
- Az első ajtóhoz
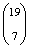 -féleképp mehetnek az utasok, a negyedik ajtónál
-féleképp mehetnek az utasok, a negyedik ajtónál
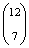 lehetőség van. A második ajtónál
lehetőség van. A második ajtónál 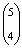 , a harmadik ajtónál 1 a lehetőség.
, a harmadik ajtónál 1 a lehetőség.
A kedvező esetek száma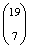 ×
× 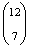 ×
×
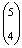 × 1=
× 1= 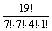 , ami 19 elem ismétléses permutációinak
száma 7, 7, 4 egyforma elem esetén.
, ami 19 elem ismétléses permutációinak
száma 7, 7, 4 egyforma elem esetén.
P(B= 7/I, 4/II, 1/III, 7/IV)=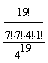 P(B)
P(B) 0,00073.
0,00073.
48.
 Egy paprikaszállítmány 1%-a romlik meg, mire a piacra eljut. Egy zsákban 300 darab paprika van. Megveszünk belőle
100 darabot. Mennyi a valószínűsége, hogy
Egy paprikaszállítmány 1%-a romlik meg, mire a piacra eljut. Egy zsákban 300 darab paprika van. Megveszünk belőle
100 darabot. Mennyi a valószínűsége, hogy
- nem lesz közöttük romlott paprika;
- pontosan 1 romlott paprika lesz;
- az összes romlottat megvettük?
Megoldás:
300 darab paprikából 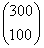 féleképpen választhatunk ki 100 darabot, hiszen a kiválasztás sorrendjére nem kell tekintettel
lennünk.
féleképpen választhatunk ki 100 darabot, hiszen a kiválasztás sorrendjére nem kell tekintettel
lennünk.
- Ha egyáltalán nem lesz romlott a paprikák között, akkor mind a 100-at a 297 darab hibátlan paprikából vettük,
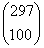 féleképpen.
féleképpen.
A keresett valószínűség:
P(A = nincs romlott)=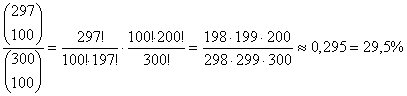
- Ha a paprikák közül 1 darab romlott, akkor ezt a 1-et a 3 db romlottból, a fennmaradó 99-et a 297 db hibátlanból
választottuk
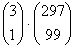 féleképpen.
féleképpen.
P(B = 1 romlott)=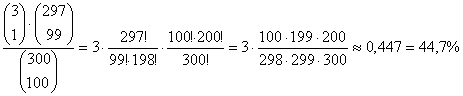
- Ha az összes romlottat megvettük, akkor 3 db romlott paprika mellé 97 db hibátlant is vettünk a 297 db közül
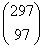 féleképpen.
féleképpen.
P(C = az összes romlott)=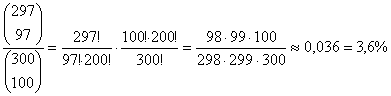 .
.
hogy a 100 db paprika között egyetlen romlott sem lesz29,5%,
hogy 1 db romlott lesz 44,7%,
hogy minden romlott köztük lesz 3,6%.
49.
Egy bizonyos fajta facsavar gyártásakor végzett minőségellenőrzés kétféle hibát mutatott ki. 400 megvizsgált csavar
közül 20 darabnak a menete volt hibás, 28 darabnak a szára rövidebb volt a megengedettnél. A megvizsgált csavarok közül
8 darabon mindkét hibát felfedezték. Feltételezhető, hogy a gyártás során mindig ilyen arányban fordulnak elő a hibás
darabok.
Mennyi annak a valószínűsége, hogy egy véletlenszerűen kiválasztott facsavar hibátlan?
Megoldás:
400 darab közül 20-nak rossz a menete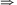 P(M=menet rossz)=
P(M=menet rossz)= 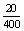 = 0,05
P(M)=5%
= 0,05
P(M)=5%
400 darab közül 28-nak rövid a szára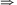 P(R=rövid a szár)=
P(R=rövid a szár)= 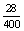 =0,07
P(R)=7%
=0,07
P(R)=7%
400 darab közül 8-nak a menete és szára is hibás P(M
P(M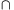 R)=
R)= 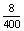 =0,02
P(M
=0,02
P(M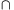 R)=2%
R)=2%
Annak a valószínűsége, hogy egy darab hibás, kiszámítható a P(M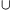 R)=P(M)+P(R)-P(M
R)=P(M)+P(R)-P(M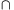 R) összefüggés alapján.
R) összefüggés alapján.
P(M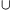 R=hibás a csavar)=0,05+0,07-0,02=0,1
(M
R=hibás a csavar)=0,05+0,07-0,02=0,1
(M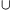 R)=10%
R)=10%
A hibás vagy a hibátlan csavar kiválasztása teljes eseményrendszert alkot, ezért
P(= nem hibás a csavar)=1-P(M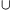 R)=1-0,1=0,9
P(
R)=1-0,1=0,9
P(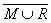 )=90%
)=90%
90% a valószínűsége annak, hogy a véletlenszerűen kiválasztott facsavar nem hibás.
50.
Egy zeneiskolában a hatodik évfolyamon kilencen zongorázni, nyolcan hegedülni, öten fuvolázni tanulnak. Mekkora annak a valószínűsége, hogy a 22 hallgatóból véletlenszerűen kiválasztott öt diák között pontosan egy tanul zongorázni?
Megoldás:
A lehetséges esetek száma 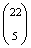 .
.
A kedvező esetekben 1 zongorista mellé 4 tanulót választottak a 8 hegedűs és az 5 fuvolás közül. Ez az alábbi
ötféle összeállításban lehetséges:
| hegedül | 4 | 3 | 2 | 1 | 0 |
| fuvolázik | 0 | 1 | 2 | 3 | 4 |
| választási lehetőségek száma (a hegedűsök és fuvolások választása egymástól független) | 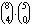 | 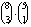 | 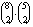 |
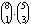 | 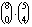 |
A különböző összeállítások egymást kizárják, és a 9 zongorista bármelyike lehet a kiválasztott a négyfős csoportoktól
függetlenül.
Ezért a kedvező esetek száma: 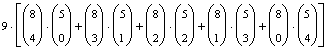 .
.
P(A=egy zongorista)= 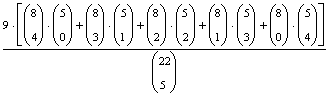
 0,244.
0,244.
A keresett valószínűség 24,4%.
51.
Nyolc egyforma bábut találomra elhelyezünk egy sakktáblán. Mennyi annak a valószínűsége, hogy mind a nyolc sorban és mind a nyolc oszlopban pontosan egy-egy bábu lesz?
Megoldás:
A lehetséges esetek száma 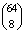 , mert a 8 bábu ennyiféleképp helyezkedhet
el a 64 mezőn.
, mert a 8 bábu ennyiféleképp helyezkedhet
el a 64 mezőn.
A kedvező esetek összeszámlálásához először azt képzeljük el, hogy egyesével, sorban egymás után helyezzük el a
bábukat a táblán. Az első bábut a 64 mező bármelyikére tehetjük, a másodikat már csak 49 mező valamelyikére rakhatjuk
le, hiszen az elsőként lerakott bábu sorában és oszlopában levő 15 mezőre nem kerülhet újabb figura. Általában, ha egy
n × n=n2 mezőből álló táblán minden sorban és oszlopban n mező van, és minden sorban és oszlopban pontosan egy bábu lehet, akkor egyet bárhova
elhelyezve, 2n-1 mezőre nem kerülhet további bábu, viszont n2-(2n-1)=(n-1)2 mezőre igen. Ezek
szerint a nyolc bábu elhelyezésére rendre 64, 49, 36, 25, 16, 9, 4, 1 mező áll rendelkezésre. (Hiszen egy bábu lerakása után a még felhasználható mezők egy 7×7-es táblát alkotnak, két bábu lerakása után a még felhasználható mezők egy 6×6-os táblát, és így tovább. Az egyes bábuk lerakása
egymástól független, így 64 × 49 × 36 × 25 × 16 × 9 × 4 × 1 eset adódik.
A feladat szerint a bábuk nem különböztethetők meg, s elhelyezésük sorrendje sem számít. Mivel 8 bábunak 8!
sorrendje van, minden megfelelő elrendezést 8!-szor vettünk figyelembe. Ezért a kedvező esetek száma 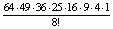 .
.
P(A=minden sorban és oszlopban pontosan egy bábu)=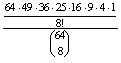
 0,0000091.
0,0000091.
A keresett valószínűség 9,1 × 10-4%.
52.
A kirándulás túraútvonalának kiválasztásához sorsolást tartottak az osztályban.
1-től 12-ig felírták a természetes számokat egy-egy cédulára, és elhelyezték egy kalapban. Kétszer húztak a kalapból,
de a cédulát visszatették az első húzás után. A húzott számtól függően haladtak az ábra szerinti fadiagramon. Igazságos
volt-e így a sorsolás?
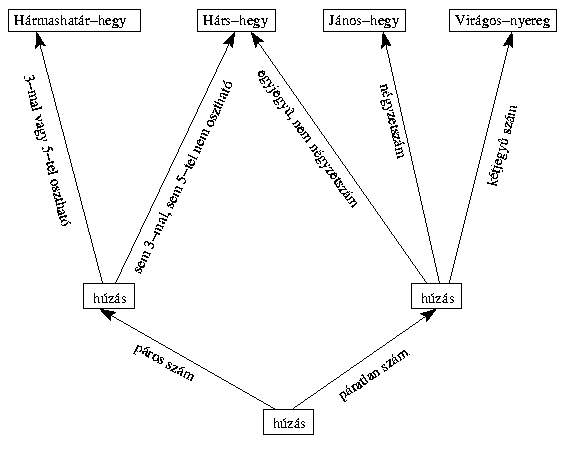
Megoldás:
Számítsuk ki az egyes útvonalak kisorsolásának valószínűségét. Mivel a cédula visszakerült a kalapba, az első és a
második húzás egymástól független volt, ezért a megfelelő valószínűségek összeszorzódnak.
A1 B1 C1
A Hármashatár-hegy lehetősége:
P(A1=páros szám)= 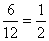 , mert 6db páros szám van a 12db cédulán.
, mert 6db páros szám van a 12db cédulán.
P(B1=3-mal v. 5-tel oszth.)= 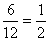 , mert 6db 3-mal vagy 5-tel osztható szám van a 12db cédulán (3; 6; 9; 12; 5; 10).
, mert 6db 3-mal vagy 5-tel osztható szám van a 12db cédulán (3; 6; 9; 12; 5; 10).
P(C1= Hármashatár-hegy)=P(B1)P(A1)= 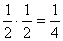 =0,25=25%
=0,25=25%
A Hárs-hegy lehetősége: Két ágon is ezt a lehetőséget sorsolhatjuk: egyrészt akkor, ha páros szám után sem 3-mal, sem
5-tel nem osztható számot húzunk, másrészt akkor, ha páratlan szám után egyjegyű, de nem négyzetszámot húzunk. E két esemény
egymást kölcsönösen kizáró, ezért a megfelelő valószínűségek összeadódnak.
P(B2= sem 3-mal, sem 5-tel nem oszth.)= 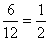 , mert 6db sem 3-mal sem 5-tel nem osztható szám van a 12db cédulán
(1; 2; 4; 7; 8; 11).
, mert 6db sem 3-mal sem 5-tel nem osztható szám van a 12db cédulán
(1; 2; 4; 7; 8; 11).
P(B2)P(A1)= 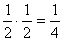
P(B3 = egyjegyű, nem négyzetszám)= 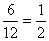 , mert 6db egyjegyű szám van, ami nem négyzetszám a 12db cédulán (2; 3; 5; 6; 7; 8).
, mert 6db egyjegyű szám van, ami nem négyzetszám a 12db cédulán (2; 3; 5; 6; 7; 8).
P(A2 = páratlan szám)= 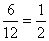 , mert 6db páratlan szám van a 12db cédulán.
, mert 6db páratlan szám van a 12db cédulán.
P(B3)P(A2) = 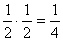
P(C2 = Hárs-hegy)=P(B2)P(A1)+P(B3)P(A2)= 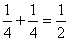 =0,5=50%
=0,5=50%
A János-hegy lehetősége:
P(B4 = négyzetszám)= 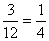 , mivel 3db négyzetszám van a 12db cédulán (1; 4; 9).
, mivel 3db négyzetszám van a 12db cédulán (1; 4; 9).
P(C3 = János-hegy)=P(B4)P(A2)= 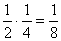 =0,125=12,5%
=0,125=12,5%
A Virágos nyereg lehetősége:
P(B5 = kétjegyű szám)= 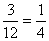 , mivel 3 db kétjegyű szám van a 12db cédulán (10; 11; 12)
, mivel 3 db kétjegyű szám van a 12db cédulán (10; 11; 12)
P(C4= Virágos nyereg)=P(A2)P(B5)= 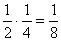 =0,125=12,5%
=0,125=12,5%
A Hármashatár-hegyre vezető túrát 25% valószínűséggel, a Hárs-hegyre vezető túrát 50% valószínűséggel, a
János-hegyre illetve a Virágos nyeregbe vezető túrát pedig 12,5-12,5% valószínűséggel sorsolhatják ki. A négy
lehetőségnek nem egyenlő az esélye, a sorsolás nem igazságos.
53.
Az iskola öt lányból és négy fiúból álló csapata tanulmányával bejutott egy környezetvédelmi verseny döntőjébe, ahol sorsolással kialakított három munkacsoportban kell dolgozniuk. Ketten riportot készítenek a tanulmányban bemutatott területért felelős szakemberrel, hárman a területről megjelent fotók és újságcikkek alapján írnak a környezeti problémákról, négyen pedig megfigyeléseket, méréseket végeznek a terület élővilágával kapcsolatban.
- Mennyi annak a valószínűsége, hogy a négy fiú alkot egy munkacsoportot?
- Mennyi a valószínűsége annak, hogy a két legfiatalabb lány egy munkacsoportba kerül?
Megoldás:
Az összes lehetőség a sorsoláson 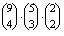
- A négy fiú csak akkor lehet együtt, ha a négy mérést végzőt közülük választják, és ettől függetlenül a háromfős
csoportot az öt lány közül sorsolják, míg a másik két lány alkotja a harmadik csoportot.A kedvező esetek száma
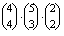 .
.
P(A=négy fiú egy csoportban)=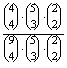 =
= 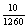
 0,008 P(A)
0,008 P(A) 0,8%
0,8%
A valószínűséget kiszámíthatjuk úgy is, hogy csak a fiúk lehetőségeit vesszük figyelembe. Az összes eset így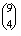 , a kedvező esetek száma 1. P(A)=
, a kedvező esetek száma 1. P(A)= 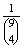 =
= 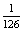
 0,008
0,008
- A három csoport bármelyikében együtt lehet a két legfiatalabb lány, ezek egymást kizáró lehetőségek. A másik hét
diák közül kell kiválasztani e csoport többi tagját és a másik két csoportot. Ha a kétfős csoportot alkotja a két lány,
akkor
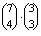 a lehetőségek száma, ha a háromfős csoportban vannak együtt, akkor
a lehetőségek száma, ha a háromfős csoportban vannak együtt, akkor
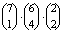 lehetőség van, ha a négyfős csoportba kerültek, akkor
lehetőség van, ha a négyfős csoportba kerültek, akkor
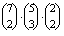 eset lehetséges.
eset lehetséges.
P(B=két adott lány együtt)=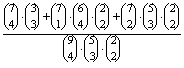 =
= 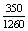
 0,278 P(B)
0,278 P(B) 27,8%.
27,8%.
54.
A 3, 3, 3, 0, 0, 5 számokat tartalmazó kártyákból húzunk. A húzás sorrendjében egymás mellé tesszük a kártyákat. Mennyi a valószínűsége, hogy a kapott hatjegyű szám
- páratlan;
- tízzel osztható;
- néggyel osztható;
- hárommal osztható;
- öttel osztható?
Megoldás:
A fenti kártyákból összeállítható hatjegyű számokat két csoportra oszthatjuk.
A 3-assal kezdődő számokból 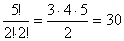 féle van (5 elem közül 2 db 3-as, 2db 0 és 1 db 5-ös ismétléses permutációinak száma).
féle van (5 elem közül 2 db 3-as, 2db 0 és 1 db 5-ös ismétléses permutációinak száma).
A 5-össel kezdődő számokból 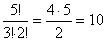 féle van (5 elem közül 3 db 3-as és 2 db 0 ismétléses permutációinak száma).
féle van (5 elem közül 3 db 3-as és 2 db 0 ismétléses permutációinak száma).
Így a lehetséges esetek száma a kettő összege: 30+10=40 .
- Akkor kapunk páratlan számot, ha az 5-re vagy 3-ra végződik. Az 5-re végződők száma egyenlő a 3; 3; 3; 0; 0
számkártyákból kirakható ötjegyű számok számával,
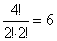 -tal (csak 3-assal
kezdődhet, 2 db 3-as és 2db 0 ismétléses permutációinak száma).
-tal (csak 3-assal
kezdődhet, 2 db 3-as és 2db 0 ismétléses permutációinak száma).
A 3-ra végződő számok kezdődhetnek 3-mal, az ilyenekből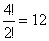 van (4 db
elemből 2 db 0, 1db 3-as, 1db 5-ös), vagy kezdődhetnek 5-tel, az ilyenekből pedig
van (4 db
elemből 2 db 0, 1db 3-as, 1db 5-ös), vagy kezdődhetnek 5-tel, az ilyenekből pedig 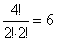 van
(4 db elemből 2 db 3-as és 2 db 0). Így a páratlan számokra vonatkozóan a kedvező esetek száma 6+12+6=24 .
van
(4 db elemből 2 db 3-as és 2 db 0). Így a páratlan számokra vonatkozóan a kedvező esetek száma 6+12+6=24 .
A keresett valószínűség:
P(A = páratlan szám)=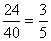 =0,6=60%
=0,6=60%
- Akkor kapunk 10-zel osztható számot, ha utoljára a 0-t tettük le. Az így kapható számok két csoportra oszthatók:
A 3-mal kezdődők esetében 2db 3-ast, 1db 0-t és 1db 5-öst kell elhelyeznünk a középső helyekre. Ezt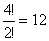 féleképpen tehetjük.
féleképpen tehetjük.
Az 5-tel kezdődők esetében 3db 3-ast és 1db 0-t kell elhelyeznünk a középső helyekre.
Ezt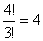 féleképpen tehetjük meg.
féleképpen tehetjük meg.
Így a 10-zel osztható számokra vonatkozóan a kedvező esetek száma: 12+4=16
A keresett valószínűség:
P(B = 10-zel osztható szám)=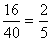 =0,4=40%
=0,4=40%
Megjegyzés: Ezekből a kártyákból vagy 10-zel osztható számokat vagy páratlan számokat lehet képezni. E két esemény teljes eseményrendszert alkot, így P(B)=1-P(A)=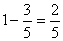
- Akkor kapunk 4-gyel osztható számot, ha az utolsó két hely mindegyikére a 0 kártya kerül. Ebben az esetben az
első négy helyre 3db 3-ast és 1db 5-öst kell elhelyeznünk. Ezt
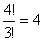 féleképpen
tehetjük, ez tehát a kedvező események száma.
féleképpen
tehetjük, ez tehát a kedvező események száma.
A keresett valószínűség:
P(C = 4-gyel osztható szám)=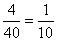 =0,1=10%
=0,1=10%
- Akkor kaphatunk 3-mal osztható számot, ha a kártyákon álló számok összege osztható 3-mal. A feladatban ez az
összeg 3+3+3+5+0+0=14, ami nem osztható 3-mal,így ezekből a kártyákból 3-mal osztható számot kirakni a lehetetlen esemény.
A keresett valószínűség:
P(D = 3-mal osztható szám)=0 - Akkor kapunk 5-tel osztható számot, ha az utolsó helyre a 0 kártya vagy az 5-ös kártya kerül.
Ha az 5-ös van a végén, akkor az első helyen csak a 3-as állhat, és a lehetőségek számát a 2db 3-as és a 2db 0 egymás közti sorrendje szabja meg, azaz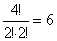 db 5-re végződő szám van.
db 5-re végződő szám van.
Ha a 0 van a végén, akkor a szám kezdődhet 3-assal és 5-össel.
A 3-assal kezdődők száma a 3; 3; 0; 5 számok lehetséges permutációinak számával egyenlő, azaz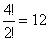 .
.
Az 5-össel kezdődők száma a 3; 3; 3; 0 számok lehetséges permutációinak számával egyenlő, azaz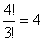 .
.
Az 5-tel oszthatóság szempontjából kedvező esetek száma 6+12+4=22
A keresett valószínűség:
P(E = 5-tel osztható szám)=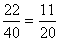 =0,55=55%
=0,55=55%
40% a valószínűsége annak, hogy a kapott hatjegyű szám 10-zel osztható,
10% a valószínűsége annak, hogy a kapott hatjegyű szám 4-gyel osztható,
0 a valószínűsége annak, hogy a kapott hatjegyű szám 3-mal osztható,
55% a valószínűsége annak, hogy a kapott hatjegyű szám 5-tel osztható.
55. Emma, Fanni, Gitta és Hanna társasjátékhoz készülődik. Sorban egymás után dobnak egyet egy szabályos dobókockával - akár több körben is -, mert az lesz közülük a kezdő, aki elsőként dob hatost.
- Mekkora valószínűséggel lesznek kezdők egy-egy kockadobás után az egyes résztvevők?
- Mekkora annak a valószínűsége, hogy nem tudják elkezdeni a játékot egy kör után?
- Számítsuk ki mind a négy résztvevő esetében annak a valószínűségét, hogy négyük közül éppen ő kezdhet!
Megoldás:
- Szabályos dobókockával a hat szám dobásának a valószínűsége egyenlő, ezért P(6)=
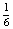 .
.
Annak a valószínűsége, hogy egy dobás nem hatos P(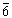 =1
=1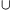 2
2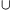 3
3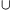 4
4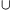 5)=1-
5)=1-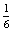 =
=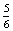 .
.
Az első körben Emma lesz a kezdő, ha hatost dob. Fanni akkor lesz kezdő, ha Emma nem hatost dobott, neki pedig elsőre sikerült.Gitta lesz a kezdő, ha előtte ketten nem dobtak hatost. Hanna kezdhet, ha a másik három játékos nem dobott hatost, ő viszont igen.
A dobások egymástól független események.
P(E=Emma kezd egy dobás után)=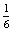
 0,167
P(E)
0,167
P(E) 16,7%
16,7%
P(F=Fanni kezd egy dobás után)=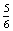 ×
× 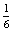 =
= 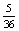
 0,139
P(F)
0,139
P(F) 13,9%
13,9%
P(G=Gitta kezd egy dobás után)=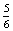 ×
× 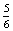 ×
× 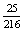 =
= 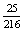
 0,116
P(G)
0,116
P(G) 11,6%
11,6%
P(H=Hanna kezd egy dobás után)=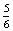 ×
× 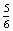 ×
× 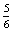 ×
× 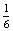 =
= 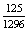
 0,096
P(H)
0,096
P(H) 9,6%
9,6%
- Az első körben nem kezdődhet el a társasjáték, ha a négy játékos egyike sem dobott hatost.
P(N=az első körben senki nem dobott hatost)=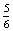 ×
× 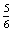 ×
× 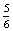 ×
× 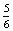
 0,482
P(N)
0,482
P(N) 48,2%
48,2%
- A kockadobásos sorsolás eredményeképpen Emma kezdhet, ha vagy az első körben vagy a második körben vagy a
harmadikban ... és így tovább... dob először hatost, amelyek egymást kizáró események, s előtte a többiek minden dobása
nem hatos volt.
P(EK=Emma kezd)=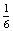 +
+ 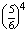 ×
×
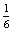 +
+ 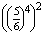 ×
×
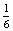 +...+
+...+ 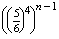 ×
×
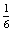 +...=
+...= 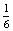 ×
× 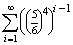
A valószínűség egy konvergens mértani sor összegének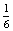 -szorosa, ahol a1=1 és q=
-szorosa, ahol a1=1 és q= 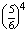 <1.
<1.
P(EK)=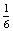 ×
× 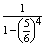 =
= 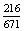 P(EK)
P(EK) 32,2%,
32,2%,
Hasonlóan kiszámítható, hogy
P(FK=Fanni kezd)=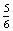 ×
× 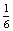 ×
× 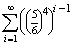 =
= 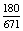 P(FK)
P(FK) 26,8%,
26,8%,
P(GK=Gitta kezd)=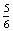 ×
× 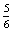 ×
× 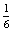 ·
· 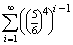 =
= 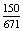 P(GK)
P(GK) 22,4%,
22,4%,
P(HK=Hanna kezd)=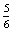 ·
· 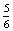 ×
× 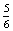 ·
· 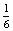 ×
× 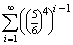 =
= 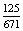 P(HK)
P(HK) 18,6%.
18,6%.
Gondoljuk meg, hogy bármelyik körben P(A)=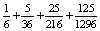 =
= 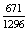 a valószínűsége annak, hogy elkezdődhet a játék. A kérdezett értékek
a valószínűsége annak, hogy elkezdődhet a játék. A kérdezett értékek
P(EK)=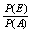 =
= 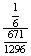 =
= 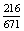 ;
;
P(FK)=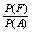 =
= 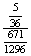 =
= 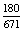 ;
;
P(GK)=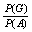 =
= 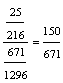 ;
;
P(HK)=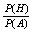 =
= 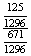 =
= 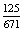 .
.
56.
 A zöldségeshez narancs- és banánszállítmány érkezett. A hosszú szállítás során a narancsszállítmány negyede veszített
az értékéből, a banánszállítmány 60%-a túlérett, a gyümölcsök többi része első osztályú maradt. Kirakodás előtt
véletlenszerűen kivettek egy gyümölcsöt valamelyik szállítmányból. Azt a darabot első osztályúnak találták, ezért
visszatették a helyére. Mennyi a valószínűsége annak, hogy ha ugyanabból a gyümölcsfajtából megint kivesznek egy
darabot, az ismét első osztályú lesz?
A zöldségeshez narancs- és banánszállítmány érkezett. A hosszú szállítás során a narancsszállítmány negyede veszített
az értékéből, a banánszállítmány 60%-a túlérett, a gyümölcsök többi része első osztályú maradt. Kirakodás előtt
véletlenszerűen kivettek egy gyümölcsöt valamelyik szállítmányból. Azt a darabot első osztályúnak találták, ezért
visszatették a helyére. Mennyi a valószínűsége annak, hogy ha ugyanabból a gyümölcsfajtából megint kivesznek egy
darabot, az ismét első osztályú lesz?
Megoldás:
A két szállítmányból egyforma valószínűséggel választhatunk: P(N)=P(B)= 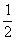 .
.
Jelölje A azt az eseményt, hogy a kiválasztott gyümölcs I. osztályú.
P(A|N=I.osztályú egy narancs)= 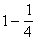 =
= 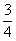 P(A|B=I.osztályú egy banán)=
P(A|B=I.osztályú egy banán)= 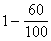 =
= 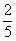
Mivel a két szállítmány közül való választás és egy gyümölcs kihúzása független esemény, első osztályú
narancsot 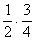 , első osztályú banánt
, első osztályú banánt 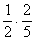 valószínűséggel
választunk egy húzásból.
valószínűséggel
választunk egy húzásból.
Egymást kizáróan vagy narancs vagy banán az első osztályú, ezért annak a valószínűsége, hogy elsőre első osztályú
árut vettünk ki 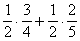 , vagyis P(A=I.osztályú a húzott gyümölcs)=
, vagyis P(A=I.osztályú a húzott gyümölcs)= 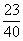 .
.
Most számítsuk ki annak a valószínűségét, hogy az elsőre kihúzott gyümölcs első osztályú narancs illetve banán volt!
P(N|A)= 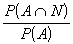 =
= 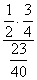 =
= 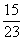 ;
illetve P(B|A)=
;
illetve P(B|A)= 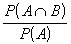 =
= 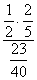 =
= 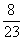 =1-P(N|A)
=1-P(N|A)
Annak a valószínűsége, hogy másodszorra ugyanabból a gyümölcsből ismét első osztályút húzunk
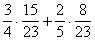 =
= 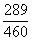
 0,628 A keresett valószínűség 62,8%.
0,628 A keresett valószínűség 62,8%.

