Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:
VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek
4. rész
1. rész 2. rész 3 rész 4. rész 5. rész 6. rész 7. rész
31.
 Egy asztalitenisz bajnokság döntőjébe három tanuló jutott be: Dani, Csaba és András. Tudjuk, hogy Dani nyerési
esélye fele Csabáénak, Csaba nyerési esélye viszont háromszor akkora, mint Andrásé. Mekkora annak a valószínűsége,
hogy a versenyt
Egy asztalitenisz bajnokság döntőjébe három tanuló jutott be: Dani, Csaba és András. Tudjuk, hogy Dani nyerési
esélye fele Csabáénak, Csaba nyerési esélye viszont háromszor akkora, mint Andrásé. Mekkora annak a valószínűsége,
hogy a versenyt
a. Dani b. András vagy Csaba nyeri?
Megoldás:
| András nyerési esélye : p | P(A) = p |
| Csaba nyerési esélye : 3p | P(C) = 3p |
Dani nyerési esélye : 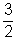 p p | P(D) = 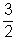 p p |
p+ 3p +
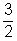 p = 1
innen p =
p = 1
innen p = 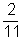 , ekkor 3p =
, ekkor 3p = 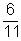 és
és 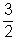 p =
p = 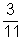 .
.
a. Tehát P(D) =
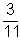 b. P(A vagy C) =
b. P(A vagy C) = 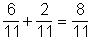 .
.
32.  Egy sakkversenyen Dezső, Feri, Anikó, Juli és Lilla vesz részt. A nyerés esélye nemenként azonos, de minden fiú
kétszer esélyesebb a nyerésre, mint bármelyik lány. Mekkora a valószínűsége annak, hogy a versenyt
Egy sakkversenyen Dezső, Feri, Anikó, Juli és Lilla vesz részt. A nyerés esélye nemenként azonos, de minden fiú
kétszer esélyesebb a nyerésre, mint bármelyik lány. Mekkora a valószínűsége annak, hogy a versenyt
a. Feri nyeri, b. Dezső vagy Anikó nyeri, c. lány nyeri?
Megoldás:
Anikó, Juli és Lilla nyerési esélye azonos:
P(A) = P(J) = P(L) = p
Dezső és Feri nyerési esélye is azonos, és kétszer akkora, mint a lányoké:
P(D) = P(F) = 2p.
A felsorolt öt esemény közül valamelyik biztosan bekövetkezik, tehát ezek valószínűségének összege 1.
3 × p + 2 × 2p = 1 innen p = 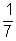
a. P(F) = 2p = 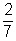 b. P(D vagy A) =
b. P(D vagy A) = 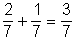
c. P(A vagy J vagy L) = 3 × 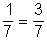 .
.
33. Hányféle három hangból álló dallam-motívum készíthető, ha az ötvonalas kottapapíron a hangjegyeket csak a vonalra illetve azok közé helyezhetjük el és a dallam ritmusát nem vesszük figyelembe? Mekkora a valószínűsége annak, hogy a három hangjegy különböző vonalra kerül?
Megoldás:
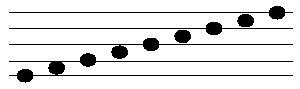 Az első kottafejet 9 helyre, a másodikat is, és a harmadikat is 9 helyre tehetjük.
Az első kottafejet 9 helyre, a másodikat is, és a harmadikat is 9 helyre tehetjük.
Ez összesen 93 lehetőség.
Ahhoz, hogy a kottafejek különböző vonalra kerüljenek, az elsőt 5, a másodikat 4, a harmadikat 3 helyre tehetjük.
Ez összesen 5 × 4 × 3 = 60 eset.
A keresett valószínűség: 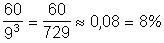 .
.
34.  A dominón 0-tól 9-ig lehetnek pöttyök (pontok). Egy dominó készletben minden lehetséges páros előfordul.
A dominón 0-tól 9-ig lehetnek pöttyök (pontok). Egy dominó készletben minden lehetséges páros előfordul.
- Hány darabból áll a teljes dominó készlet?
- Hányféleképpen lehet közülük kiválasztani kettőt úgy, hogy azok a játék szabályai szerint egymáshoz illeszthetők legyenek?
- Mekkora a valószínűsége annak, hogy a b. szerint kiválasztott párosok között van 0 pontú dominó?
Megoldás:
- Egy dominónak két lapja van, melyek mindegyikén 0-tól 9-ig lehetnek pontok. Egy lap esetén ez 10 különböző eset.
Ha a 10 különböző lap mindegyike együtt szerepel a dominókon egy másik, tőle különböző pontú lappal, akkor
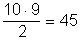 féle dominót kapunk. Ehhez adódnak azok az esetek, amikor a dominónak
mindkét lapja azonos pontú, ez még 10 eset. Összesen tehát 55 db dominóból áll a teljes készlet.
féle dominót kapunk. Ehhez adódnak azok az esetek, amikor a dominónak
mindkét lapja azonos pontú, ez még 10 eset. Összesen tehát 55 db dominóból áll a teljes készlet.
- A jó páros kiválasztásakor külön vizsgáljuk azokat az eseteket, amikor a húzott dominók között van dupla,
(mindkét lapja azonos) illetve azokat, amikor nincs dupla. Először összeszámoljuk az eseteket úgy, mintha számítana, hogy milyen sorrendben választjuk ki a két dominót, és a kapott számot utána osztjuk kettővel, hiszen valójában nem számít a sorrend.
- a)Ha elsőként dupla dominót húzunk - amit 10-féleképpen tehetünk meg- akkor másodikként ezekhez csak 9-félét
húzhatunk, ez összesen 10 × 9 = 90 eset.
b)Ugyanígy 90 olyan eset van, amikor a 2. dominó dupla. - Ha első húzásnál nem húzunk duplát, akkor 55 -10 = 45-ből választhatunk. A második húzásnál pedig a különböző lapú dominó egyik lapjához is 8 féle, másik lapjához is 8 féle, összesen 16 féle dominó választható. Például az |1,2| dominóhoz jöhet egyrészt az |1,0|; |1,3|; |1,4|; |1,5|; |1,6|; |1,7|; |1,8|; |1,9|, másrészt a |2,0|; |2,3|; |2,4|; |2,5|; |2,6|; |2,7|; |2,8|; |2,9|.
Ekkor 45 × 16 = 720 féle húzás lehetséges. A három együtt 90 + 90 + 720 = 900 eset. tehát összesen 900/2 = 450 esetben kaphatunk a feltételeknek megfelelő párost. - a)Ha elsőként dupla dominót húzunk - amit 10-féleképpen tehetünk meg- akkor másodikként ezekhez csak 9-félét
húzhatunk, ez összesen 10 × 9 = 90 eset.
- Ha az első kihúzott dominó |A,B|, és például A 0 pontú, akkor B 10 féle lehet. Ezekhez másodszorra az
első dominó A lapjához 9 félét választhatunk, ez így összesen 10 × 9 = 90 . De itt is figyelembe vettük a húzások sorrendjét, ezért valójában 90:2 = 45 lehetőség van. Az első dominóhoz választhatunk még olyan dominót is, amelyek egyik lapja B-vel egyezik meg . Ennél az esetnél a |0,0| dupla dominót nem kell számolni, mert az nem ad új párost. Így 9 féle laphoz 9 félét (mert a 0-t tartalmazó dominókat szintén már összeszámoltuk, gy azt nem vesszük bele az esetek közé) húzhatunk. Például a |0,1| dominóhoz másodszorra az |1,1|; |1,2|; |1,3|; |1,4|; |1,5|; |1,6|; |1,7|; |1,8|; |1,9| dominókat.
Ez 9 × 9 = 81 eset.
A feladat c. feltételének megfelelő párosok száma összesen: 45 + 81 = 126.
A jó párosok száma pedig összesen a feladat b. része alapján: 450.
P(a választott párosok között van 0 pontú) =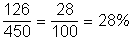 .
.
35.
Egy üzletben a kiárusításkor egy nagy kétrekeszes ládába öntik az egyforma méretű férfi zoknikat. A zoknik nincsenek összepárosítva és legfeljebb csak színükben különböznek, ezért nap végére teljesen összekeverednek. Az egyik rekeszben 60 sötétkék, 37 drapp és 51 fekete, a másik rekeszben 40 sötétkék, 63 drapp és 49 fekete zokni van. Mekkora a valószínűsége annak, hogy mindkét rekeszből egyet-egyet kivéve, egyforma a két zokni színe?
Megoldás:
A különböző rekeszekből való húzások független kísérletek. A két sötétkék, a két drapp és a két fekete zokni
húzása egymást kizáró események. Az egyik rekeszben összesen 148 zokni van, a másikban 152, ezért a keresett valószínűség
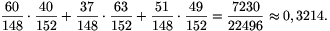
A valószínűség 32,14%.
36.
 A könyvespolc alsó polcáról a kétéves Pisti leszedte a könyveket, majd "saját ízlése szerint" visszarakta mind a
25-öt. Mennyi a valószínűsége annak, hogy a köztük levő három idegen nyelvű könyv egymás mellé került?
A könyvespolc alsó polcáról a kétéves Pisti leszedte a könyveket, majd "saját ízlése szerint" visszarakta mind a
25-öt. Mennyi a valószínűsége annak, hogy a köztük levő három idegen nyelvű könyv egymás mellé került?
Megoldás:
Tételezzük fel, hogy a polcra csupa különböző könyvet tettek, így 25! azok lehetséges sorrendjeinek száma.
A kedvező esetek összeszámlálásánál átmenetileg tegyük fel, hogy a három idegen nyelvű könyvet összekötöttük, és
egyetlen csomagként tesszük a polcra. Így 22 db könyvet és az előbb említett csomagot kell a polcra tennünk. Ezt
23!-féleképpen tehetjük meg. Ha a csomagot kibontjuk, a benne lévő három idegen nyelvű könyvet 3! féleképpen
cserélgethetjük. A polcon levő 23! féle sorrend mindegyikéhez 3! féle belső cserelehetőség tartozik, ezért a
kedvező kimenetelű esetek száma 23!3!
P(A = a három idegen nyelvű könyv egymás mellett van) = 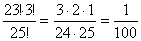
Tehát 1% a valószínűsége, hogy a visszarakáskor az idegen nyelvű könyvek egymás mellé kerülnek.
37.
 Öt pénzérme feldobásakor mennyi a valószínűsége, hogy pontosan három érmén a fej lesz felül?
Öt pénzérme feldobásakor mennyi a valószínűsége, hogy pontosan három érmén a fej lesz felül?
Megoldás:
Minden érme feldobásának kétféle kimenetele lehet. Az egyes érmék feldobása független a többitől, így az öt érmén
kialakuló összes lehetőségek száma 25.
Ha az öt érme közül 3 mutat fejet, akkor ez összesen 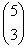 féleképpen
fordulhat elő, hiszen az érmék eltérő sorrendje nem számít különböző kimenetelnek.
féleképpen
fordulhat elő, hiszen az érmék eltérő sorrendje nem számít különböző kimenetelnek.
A keresett valószínűség:
P(A=3 érmén fej van)= 
Tehát 31,25% valószínűséggel lesz az öt közül három érmén a fej felül.
38.
Tételezzük fel, hogy egy gyermek születésekor ugyanakkora valószínűséggel lesz a csecsemő fiú illetve lány. Tudjuk, hogy egy családban öt különböző életkorú testvér közül a legidősebb gyermek lány.
- Mekkora annak a valószínűsége, hogy mind az öt gyermek lány?
- Mekkora annak a valószínűsége, hogy két lány és három fiú van a családban?
- Mekkora annak a valószínűsége, hogy a középső gyermek fiú?
Megoldás:
Az első gyermek lány, a másik négy gyermek neme kétféle lehet egymástól függetlenül.
Az összes lehetőség 24.
| a. Egyetlen esetben lesz mind az öt gyermek lány.
P(A=öt leány, ha az első lány)= 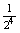 =0,0625 =0,0625 |
P(A)=6,25% |
| b. A négy kisebb gyermek egyike lány, a többi fiú. Ez 4 kedvező eset.
P(B=2lány, 3fiú, ha az első lány)= 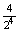 =0,25 =0,25 |
P(B)=25% |
| c. Az első gyermek lány, a harmadik fiú, a többi három vagy fiú vagy lány. Ez 23 eset.
P(C=első lány, harmadik fiú)= 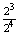 =0,5 =0,5 |
P(C)=50% |
39.
 A BKV-jegyen 3×3-as négyzetrácsban 9 mezőt találunk 1-től 9-ig számozva. A kilenc szám közül hármat lyukasztott az
automata. Mennyi a valószínűsége annak, hogy köztük van az 1-es szám?
A BKV-jegyen 3×3-as négyzetrácsban 9 mezőt találunk 1-től 9-ig számozva. A kilenc szám közül hármat lyukasztott az
automata. Mennyi a valószínűsége annak, hogy köztük van az 1-es szám?
Megoldás:
A lyukasztáskor a számok sorredjére nem kell tekintettel lennünk, így a háromlyukú számkombinációk száma összesen
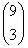 .
.
Ha az 1-es a kilyukasztott számok között van, akkor a hiányzó két szám csak a többi nyolc szám közül lehet, így a
kedvező esetek száma 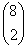 .
.
P(A = az 1-est kilyukasztottuk)= 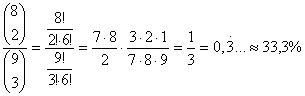 .
.
Tehát kb. 33,3% valószínűséggel lesz az 1-es a három kilyukasztott szám között.
40.
Az ötös lottón 90 számból választanak 5-öt a szelvények kitöltői. Hányszor nagyobb a valószínűsége egy négytalálatos szelvénynek, mint az öttalálatosnak?
Megoldás:
A lottószelvény kitöltésénél a kiválasztott számok sorrendjére nem kell tekintettel lennünk, ezért az összes
kitöltési lehetőségek száma: 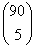 . Ezek között egyetlen öttalálatos van,
így az öttalálatos szelvény valószínűsége:
. Ezek között egyetlen öttalálatos van,
így az öttalálatos szelvény valószínűsége:
P(A = öttalálatos a lottón)=
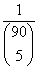 =0,000000023.
=0,000000023.
Az ötös lottón akkor érünk el négytalálatost, ha az 5 kihúzott szám közül pontosan 4 a mi számaink közül való, egy
pedig biztosan nem azok közül van, vagyis az általunk meg nem jelölt 85 szám valamelyike.
A kedvező esetek száma 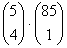 , mivel a választások egymástól függetlenek.
, mivel a választások egymástól függetlenek.
A négytalálatos szelvény valószínűsége:
P(B = négytalálatos a lottón)=
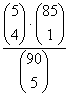 =0,00000967.
=0,00000967.
Az esélyek összehasonlítása: 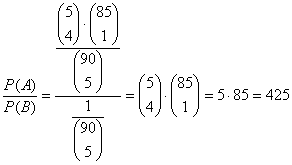
Tehát 425-ször valószínűbb az ötös lottón négy találatot elérni, mint ötöt.
41.
Az iskolai tollaslabda bajnokság rendezői 12 palack szénsavas és 10 palack szénsavmentes ásványvizet vittek a pihenőhelyre. A páros mérkőzések első szünetében a négy versenyzőnek felbontottak egy-egy palackot anélkül, hogy megnézték volna a címkéket. Mekkora a valószínűsége annak, hogy 2 szénsavas és 2 szénsavmentes palackot nyitottak ki?
Megoldás:
A lehetséges esetek száma 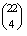 .
.
A kedvező esetekben két palackot választottak a 12 közül és kettőt a 10 közül egymástól függetlenül.
Ez 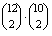 eset.
eset.
P(A=két-két palack a 12+10 közül)= 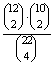 =
= 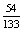
 0,406
P(A)
0,406
P(A)  40,6%
40,6%
A keresett valószínűség 40,6%.
42.
 Töhötöm elvesztette Budapesten lakó barátja telefonszámát. Arra biztosan emlékszik, hogy 2-essel kezdődik, pontosan
4 darab 3-as van benne és nincs a számjegyei között 9-es. Mennyi a valószínűsége annak, hogy már az első próbálkozása
sikerrel jár, és fel tudja hívni a barátját?
Töhötöm elvesztette Budapesten lakó barátja telefonszámát. Arra biztosan emlékszik, hogy 2-essel kezdődik, pontosan
4 darab 3-as van benne és nincs a számjegyei között 9-es. Mennyi a valószínűsége annak, hogy már az első próbálkozása
sikerrel jár, és fel tudja hívni a barátját?
Megoldás:
A hétjegyű telefonszámból az elsőt biztosan tudja Töhötöm. Az ismeretlen hat számjegy közül 4 db 3-as van, és két számjegyről nem tudunk biztosat.
- ha a hiányzó két számjegy egyforma, akkor ezek 8 féle szám közül kerülhetnek ki, hiszen az ismeretlen számjegy
sem, 9-es sem 3-as nem lehet. A lehetséges próbálkozások száma
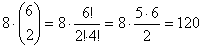 , mert 6
hely közül kell kiválasztani a két ismeretlen egyforma számjegy helyét.
, mert 6
hely közül kell kiválasztani a két ismeretlen egyforma számjegy helyét.
- ha a hiányzó két számjegy különböző, akkor azokat
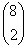 féleképpen
választhatja meg Töhötöm, majd a kiválasztás után a négy egyforma és két különböző számjegyet \(\displaystyle {6!\over4!}\) féle sorrendbe teheti. Tehát ekkor a próbálkozások száma
féleképpen
választhatja meg Töhötöm, majd a kiválasztás után a négy egyforma és két különböző számjegyet \(\displaystyle {6!\over4!}\) féle sorrendbe teheti. Tehát ekkor a próbálkozások száma
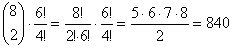
Az a. és b. lehetőségek egymást kizáró eseményeket írnak le, így összegük adja az összes lehetséges próbálkozások számát. A kedvező esetek száma 1, hiszen csak egy telefonszámon érheti el Töhötöm a barátját.
A keresett valószínűség:
P(A = sikeres hívás)=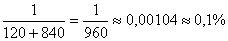 .
.
Tehát kb. 0,1% a valószínűsége annak, hogy az első próbálkozásra sikeres lesz a hívás.
43.
Egy szerencsejáték-automata három hengerén 20-20 kép van:
| I.henger | II.henger | III.henger | |
| szív | 3 | 1 | 1 |
| csillag | 0 | 3 | 4 |
| háromszög | 2 | 2 | 4 |
| kör | 2 | 4 | 4 |
| négyzet | 7 | 7 | 0 |
| lóhere | 6 | 3 | 7 |
Egy zseton bedobása után az automata megpörgeti, majd megállítja a hengereket úgy, hogy mindegyiken egy-egy kép válik láthatóvá. 500 nyereményzsetont ad ki a gép, ha három szív látható. 8 zseton a nyeremény bármely másik három egyforma kép esetén.
- Mennyi a főnyeremény elérésének valószínűsége egy-egy játékban?
- Mekkora annak a valószínűsége, hogy a nyeremény 8 zseton?
Megoldás:
- Az első hengeren
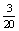 a valószínűsége annak, hogy megállás után szív
látható, a másik két hengeren pedig
a valószínűsége annak, hogy megállás után szív
látható, a másik két hengeren pedig 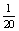 . Ezek független események.
. Ezek független események.
P(A=3 szív)=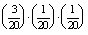
 0,000375
0,000375 0,04%.
0,04%.
- 8 zseton a nyeremény, ha három csillag vagy három háromszög vagy három kör vagy három négyzet vagy három lóhere
látható. Ezek egymást kölcsönösen kizáró események.
P(B=8 zseton a nyeremény)=0+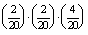 +
+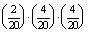 +0+
+0+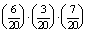
 0,022
0,022 2,2%.
2,2%.
A főnyeremény elnyerésének 0,04%, a 8 zsetonos nyeremény elérésének 2,2% a valószínűsége.
44.
Egy húszfős diákcsoport hétvégi kirándulásra indult a Nyugati pályaudvarról. Induláskor kiderült, hogy Rendetlen Tóbiás és Feledékeny Fáni elfelejtett diákigazolványt hozni, pedig a csoport minden tagjának kedvezményes jegyet váltottak. A kalauz a vonaton a csoportból három diákot szúrópróbaszerűen ellenőriz. Mennyi a valószínűsége, hogy
- Rendetlen Tóbiás köztük van;
- mindkét potyautas köztük van;
- legalább az egyiküktől kéri a kalauz a diákigazolványt?
Megoldás:
A 20 diákból 3-at szúrópróbaszerű ellenőrzésre 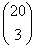 féleképpen lehet
kiválasztani.
féleképpen lehet
kiválasztani.
- Ha rendetlen Tóbiás az ellenőrzött személyek között van, akkor rajta kívül a többi 19 diák közül még kettőtől kéri el az
igazolványt a kalauz. Őket
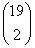 féleképpen lehet kiválasztani.
féleképpen lehet kiválasztani.
A keresett valószínűség:
P(A = Tóbiást ellenőrzik)=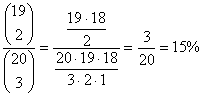
- Ha mindkét potyautas az ellenőrzött személyek között van, akkor rajtuk kívül még egy diákot választ ki a kalauz
a többi 18 közül ellenőrzésre. Ezt
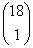 féleképpen teheti meg.
A keresett valószínűség:
féleképpen teheti meg.
A keresett valószínűség:
P(B = Tóbiást és Fánit is ellenőrzik)=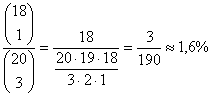
- Legalább az egyik potyautast ellenőrizni azt jelenti, hogy vagy az egyiket, vagy a másikat, vagy mindkettőjüket
ellenőrzik. Ezeken a lehetőségeken kívül még az is előfordulhat, hogy egyikük sincs az ellenőrzöttek között. E négy
esemény teljes eseményrendszert alkot, így az első három bekövetkezésének valószínűségét megkaphatjuk, ha a
negyedik esemény valószínűségét 1-ből kivonjuk.
Ha egyiküket sem ellenőrzik, akkor az ellenőrzött személyeket a 18 diáktárs közül választhatja a kalauz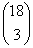 féleképpen.
féleképpen.
A kiegészítő esemény valószínűsége:
P(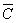 =sem T-t, sem F-t nem ellenőrzik)=
=sem T-t, sem F-t nem ellenőrzik)= 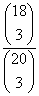
A keresett valószínűség:
P(C = legalább az egyiket)=1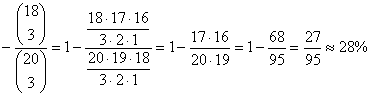
Tehát Rendetlen Tóbiás ellenőrzésének valószínűsége 15%, mindkettőjüké kb. 1,6%, és hogy legalább az egyiket ellenőrzik, az kb. 28%-os valószínűségű.
45.
Két diák hétvégi forgalomszámlálást vállalt egy olyan útszakaszon, ahol személygépkocsik és gépjárművek közlekednek.
Az adatok összesítéséből kiderült, hogy a járművek 25%-a gépjármű, 75%-a személygépkocsi egy-egy hétvégén. Megfigyelték
azt is, hogy a személy-gépkocsik kétharmadában csak a vezető ült, a gépjárművek ötödében legalább ketten ültek.
Mekkora annak a valószínűsége, hogy egy hasonló hétvégi napon ezen az útszakaszon elhaladó járműben legalább két
személy ül?
Megoldás:
Az összes jármű negyede gépjármű, és minden ötödikben legalább ketten ülnek.
Ezért P(A=gépjármű halad el és legalább ketten ülnek benne)= 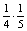
A személygépkocsik kétharmadában csak a vezető ül, harmadában legalább két ember van.
Az összes jármű háromnegyede személygépkocsi, minden harmadikban legalább ketten ülnek.
Ezért P(B=személygépkocsi halad el és legalább ketten ülnek benne)= 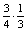
A kétféle jármű elhaladása egymást kizáró esemény, ezért P(A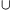 B)=P(A)+P(B)
B)=P(A)+P(B)
P(A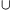 B=az elhaladó járműben legalább ketten ülnek)=
B=az elhaladó járműben legalább ketten ülnek)= 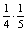 +
+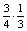 =
= 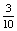
P(A B)=30% a keresett valószínűség.
B)=30% a keresett valószínűség.

