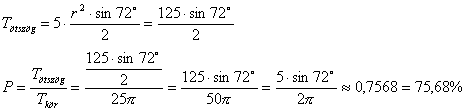Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:
VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek
6. rész
1. rész 2. rész 3 rész 4. rész 5. rész 6. rész 7. rész
A valószínűség geometriai kiszámítási módja
A valószínűség-számítási feladatok egy részében az elemi eseményeket egy geometriai alakzat pontjaihoz rendeljük hozzá, és feltételezzük, hogy egy eseményhez tartozó ponthalmaz mértéke (hossza, területe, térfogata) arányos az esemény valószínűségével. Most erre mutatunk néhány feladatot.
57. Pistike életében először mászott föl testnevelés órán a 4,2m magas mászórúdra. Mennyi annak a valószínűsége, hogy az utolsó 1 méteren ment a kezébe a szálka?
Megoldás:
A 4,2m magas mászórudat először 1,6m magasan fogta meg, ezért csak a maradék 4,2m-1,6m=2,6m-es rúddarabbal
foglalkozunk.
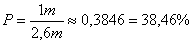
Megjegyzés: A feladat nem volt pontosan megfogalmazva: az 1,6 métert önkényesen választottuk.
58. Egy intervallum belsejében véletlenszerűen kiválasztok egy P pontot. Mennyi a valószínűsége annak, hogy a P pont közelebb van a felezőponthoz, mint bármelyik végponthoz?
Megoldás:
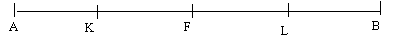
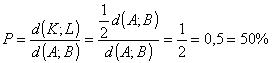
59.
A méterrúd piros és fehér 10 cm-es szakaszokból áll, melyek egymást váltják és az első szakasz piros színű. A rúd 32 cm-nél kettétört.
- Ha rámászik egy hangya, akkor a két rész közül melyiken lesz nagyobb az esélye, hogy piros színű szakaszon telepszik le?
- Mérgünkben a hosszabb szakaszt félbetörjük. Most a három rész közül melyiken találjuk legnagyobb valószínűséggel piros színű részen a hangyát?
Megoldás:
Rajzoljuk le a méterrudat:
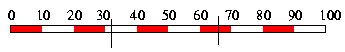
- Az első rész 32cm hosszú és ebből 20 cm a piros szakasz hossza.
Itt a hangya 20/32 = 62.5%-os valószínűséggel lesz piros részen.
A rúd másik fele 68cm-es, és ebből 30cm piros, így ezen a szakaszon csak 30/68=44% a piros részen tartózkodás valószínűsége. Tehát az első részen nagyobb a keresett valószínűség. - A hosszabb szakaszon a törés a 66cm-nél lesz.
Az első szakaszon a valószínűség változatlanul 20/32 = 62,5%.
A második szakaszon 16cm piros rész van, és ez a szakasz 34cm. Így a keresett valószínűség: 16/34 = 47%.
A harmadik szakasz is 34cm hosszú, és itt a piros rész csak 14 cm. Ezért a valószínűség 14/34 = 41%.
Most is az első szakaszon a legnagyobb a keresett valószínűség. Észrevehetjük azt is, hogy a három darabja a méterrúdnak majdnem egyforma hosszú, ennek ellenére a valószínűségek nagyon eltérnek egymástól.
60.
Mennyi a valószínűsége, hogy ha felírunk egy számot 0 és 1 között, akkor 5-ös számjegy lesz a
| a. tizedek | b. századok | c. ezredek helyén? |
Megoldás:
Célszerű a számokat számegyenesen szemléltetni.
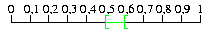
A tizedek helyén akkor szerepel 5-ös számjegy, ha a szám a 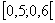 intervallumban van.
intervallumban van.
A 0 és 1 közötti számok egy 1 hosszúságú intervallum pontjainak feleltethetők meg, míg a keresett számok egy 0,1
hosszúságú intervallumban vannak.
Innen: 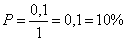
A századok helyén akkor szerepel 5-ös számjegy, ha a szám a 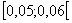 ,
,
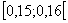 ,...,
,...,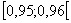 intervallumok
valamelyikében van.
intervallumok
valamelyikében van.
A kedvező intervallumok összes hosszúsága: 10×0,01=0,1.
A keresett valószínűség ebben az esetben is:
P=0,1
Hasonló gondolatmenettel jutunk ugyanerre az eredményre, hiszen most 100×0,001=0,1 a kedvező intervallumok hosszúsága.
Észrevehetjük, hogy a feladat eredménye nem függ attól, hogy az 5-ös számjegyet vizsgáltuk, és attól sem, hogy
melyik helyiértéken.
61.
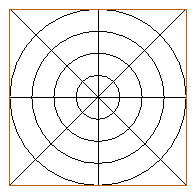 Egy pók az ábrán látható módon szőtte be a 40cm × 40cm-es pinceablakot.
Egy pók az ábrán látható módon szőtte be a 40cm × 40cm-es pinceablakot.
Mekkora valószínűséggel várja a pók az áldozatát a háló egyenes szakaszán?
Megoldás:
Az egyes körök sugarai 5,10,15 és 20cm-esek.
A kör kerülete:2r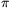
A négy kör kerületének összege = 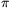 2(5+10+15+20)=100
2(5+10+15+20)=100 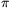 =314,16 (cm)
=314,16 (cm)
Az egyenes szakaszok hossza=2a+2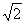 a , ahol a a négyzet 40cm-es
oldalhosszúságát jelenti.
a , ahol a a négyzet 40cm-es
oldalhosszúságát jelenti.
Így az egyenes szakaszok hossza = 80+80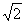 =193,14 (cm)
=193,14 (cm)
A pókháló teljes hossza: 314,16+193,14=507,3 cm.
A keresett valószínűség: 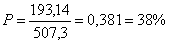
62.
 Mennyi a valószínűsége, hogy a kártyára hulló (pontszerű) morzsa éppen valamelyik rombuszon landoljon?
Mennyi a valószínűsége, hogy a kártyára hulló (pontszerű) morzsa éppen valamelyik rombuszon landoljon?
Egy kártya 86 mm hosszú és 61mm széles.
A nagyobb méretű rombuszok átlói 13 és 17mm-esek, míg a kisebbek átlói 5 és 7mm-esek.
Megoldás:
A kártya területe adja a teljes eseménynek megfelelő ponthalmazt.
T=ab=61×86=5246 (mm2)
A rombusz területe = \(\displaystyle {ef\over2}\), ahol e és f a két átlót jelöli.
A nyolc nagy rombusz területe =4×13×17=884 (mm2)
A két kis rombusz területe = 5×7= 35 (mm2)
A rombuszok összes területe = 919 (mm2)
Annak a valószínűsége, hogy valamelyik morzsa éppen egy rombuszra kerüljön:
P = 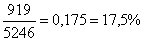
63.
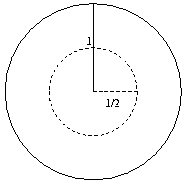 Számítsd ki a valószínűségét annak, hogy egy egységsugarú körben véletlenszerűen elhelyezett pont közelebb van a kör
középpontjához, mint a kerületéhez!
Számítsd ki a valószínűségét annak, hogy egy egységsugarú körben véletlenszerűen elhelyezett pont közelebb van a kör
középpontjához, mint a kerületéhez!
Megoldás:
Egy egységsugarú kör belsejében azok a pontok, melyek egyenlő távol vannak a középpontjától és a kerületétől,
egy 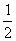 sugarú kör kerületének pontjai. Ezen a körön belül levő
pontok vannak a körök középpontjához közelebb.
sugarú kör kerületének pontjai. Ezen a körön belül levő
pontok vannak a körök középpontjához közelebb.
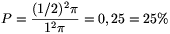
64.
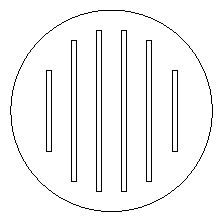 Mennyi a valószínűsége annak, hogy Peches Panka fülbevalójából a drágakő éppen beleessen a fürdőszoba lefolyóba, ha a
tragikus esemény, azaz a kő kipottyanása pontosan a lefolyó fölött következett be. A lefolyó egy 10cm sugarú kör,
melyen a nyílások 0,5cm szélesek és 8, 14, illetve 16cm hosszúak.
Mennyi a valószínűsége annak, hogy Peches Panka fülbevalójából a drágakő éppen beleessen a fürdőszoba lefolyóba, ha a
tragikus esemény, azaz a kő kipottyanása pontosan a lefolyó fölött következett be. A lefolyó egy 10cm sugarú kör,
melyen a nyílások 0,5cm szélesek és 8, 14, illetve 16cm hosszúak.
Megoldás:
A drágakövet kicsiny mérete miatt pontszerűnek tekinthetjük.
A lefolyóba a hat téglalap alakú lyukon kerülhet a drágakő.
Ezek területének összege:
T= 2 (ab+ac+ad), ahol a az egyes téglalapok közös 0,5cm-es szélessége, míg b=8cm, c=14cm és d=16cm.
Ez a terület: 2×0.5×(8+14+16)= 38 (cm2)
A lefolyó egy 10 cm sugarú kör, melynek területe:
T= r2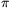 =100
=100 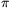 =314,16(cm2)
=314,16(cm2)
Annak a valószínűsége, hogy a drágakő beleesik a lefolyóba:
P= 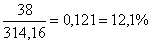
65.
Egységnyi oldalú szabályos háromszög oldalait
| a. megfelezzük | b. elharmadoljuk | c. elnegyedeljük | d. n egyenlő részre osztjuk |
Mennyi a valószínűsége annak, ha a háromszög belső tartományában véletlenszerűen kijelölünk egy pontot, akkor az a kis háromszögek valamelyikében lesz?
Megoldás:

Elegendő egy kis háromszög területét meghatározni, és a kapott eredmény területét kell háromszorozni.
A kis háromszögek hasonlóak az eredeti szabályos háromszöghöz, és a hasonlóság aránya az egyes esetekben:
| a. 1 | b. 1/3 | c. 1 | d. 1/n |
| a. 1/4-ed | b. 1/9-ed | c. 1/16-od | d. 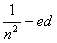 része. része. |
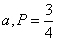 = 75% = 75% | b. 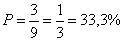 | c. 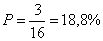 | d. 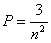 |
66.
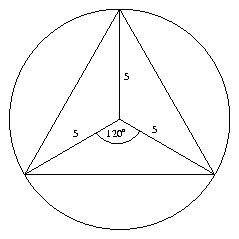
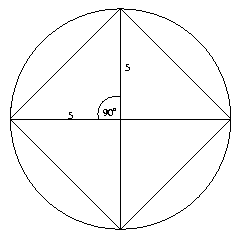
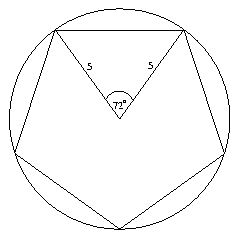
Egy 5 cm sugarú körbe szabályos
Mennyi a valószínűsége annak, hogy ha találomra kijelölünk egy pontot a kör belső tartományában, akkor az egyben a fenti sokszögek belső tartományába is esik? Megoldás: A valószínűséget a beírt sokszög területének és a teljes kör területének aránya adja.
|
|
67.
Egy 6 cm sugarú kör köré és bele is szabályos háromszöget írunk. Mekkora a valószínűsége annak, ha véletlenszerűen kiválasztunk az ábrán egy pontot, akkor az
- a külső háromszög és a kör közé;
- a kör és a belső háromszög közé;
- a belső háromszögbe esik?
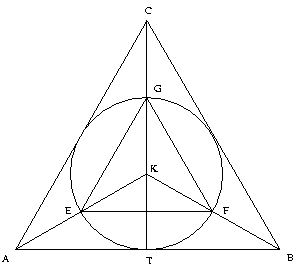 Megoldás:
Megoldás:
A kérdéses területek meghatározásánál az ábra jelöléseit használjuk.
A kör középpontja az ABC háromszög súlypontja, ezért a CT=3r=18 cm.
Az ATK háromszög egy szabályos háromszög fele, ezért AT=6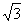 .
.
Az ABC háromszög területe:
 108
108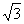 cm2 (187,06cm2 )
cm2 (187,06cm2 )
A kör területe:
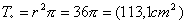
- A külső háromszög és a kör közötti terület:

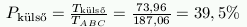
- A belső háromszög területe:
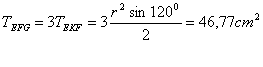
A kör és a belső háromszög közötti terület:
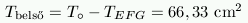
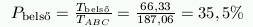
- Annak a valószínűsége, hogy a kiválasztott pont a belső háromszögbe esik:
\(\displaystyle P_{EFG}={T_{EFG}\over T_{ABC}}={46,77\over187,06}=25\%\)
68.
Egy csempézett padló szabályos hatszögekből áll. Mi az esélye annak, hogy egy gomb a hatszög belsejébe essen? Legyen a hatszög oldala 12cm, a gomb átmérője pedig 4cm.
Megoldás:
Ha a gomb középpontja közelebb van a hatszög valamely oldalához, mint 2cm, akkor a gomb nincs teljes terjedelmével egy hatszög belsejében. Tehát a számunkra "kedvező" hely a gomb középpontja számára egy olyan hatszög belsejében van, melynek oldalai 2cm-rel közelebb vannak a hatszög középpontjához, mint az eredetinek. Az új és az eredeti hatszög területének aránya adja meg a keresett valószínűséget.
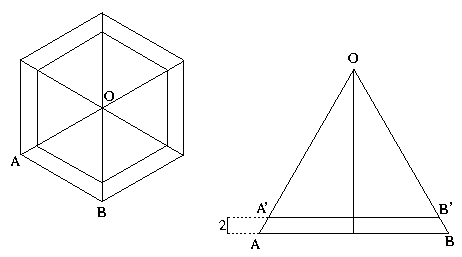 Minden hatszög felbontható hat egybevágó egyenlő oldalú háromszögre. A két hatszögben levő háromszögek területe a
hatszög területének hatodrésze, ezért elég a háromszögek területének arányát kiszámítani.
Minden hatszög felbontható hat egybevágó egyenlő oldalú háromszögre. A két hatszögben levő háromszögek területe a
hatszög területének hatodrésze, ezért elég a háromszögek területének arányát kiszámítani.
Jelöljük a hatszögek középpontját O-val, az eredeti hatszög egyik oldalát AB-vel, ennek megfelelően a kisebb
hatszög megfelelő oldalát A'B'-vel. Mint tudjuk, AB=12cm. Az ABO egyenlő oldalú háromszög magassága 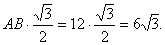
A kisebb 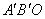 háromszög
háromszög 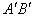 oldalhoz tartozó magassága
oldalhoz tartozó magassága 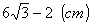 , mivel
, mivel 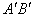 ennyivel van közelebb O-hoz, mint AB.
ennyivel van közelebb O-hoz, mint AB.
A két háromszög hasonló, így területeik aránya megegyezik a megfelelő szakaszaik arányának négyzetével:
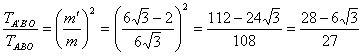
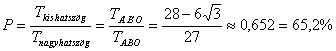
69.
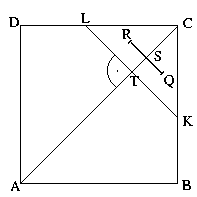
Válassz véletlenszerűen egy Q pontot egy ABCD egységnégyzet belsejében. Tükrözd az AC átlóra, a kapott pontot jelöld R-rel. Legyen S a QR szakasz felezőpontja! Mennyi a valószínűsége annak, hogy az AS távolság kisebb, mint 1?
Megoldás:
A QR szakasz szimmetrikus az AC tengelyre, tehát az S pont az AC tengelyre esik. Ha S egybeesik a T ponttal, akkor lesz az
AS távolság 1 egység. Tehát akkor lesz a Q pont "jó" helyen, ha az AC tengelyre eső merőleges vetülete az AT szakasz belsejébe
esik, tehát ha a Q pont az ABKLD ötszög belsejében van.
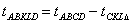
CKL háromszög egyenlő szárú derékszögű, tehát
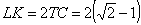
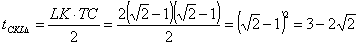
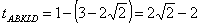
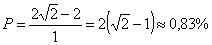


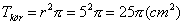
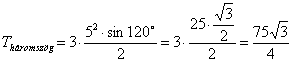
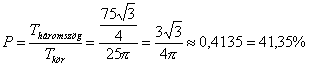

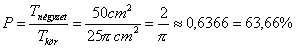
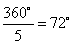 .
.