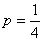Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:

VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek

7. rész

  1. rész   2. rész   3 rész   4. rész   5. rész   6. rész   7. rész

70.

Eldobunk egy labdát egy téglalap alaprajzú szobában, melynek padlója 5m széles és 10m hosszú. Mennyi a valószínűsége, hogy a labda olyan helyen áll meg, hogy középpontja közelebb van a szoba valamely sarkához, mint a szoba középpontjához?

Megoldás:

Jelöljük a szoba alaprajzának, azaz a téglalapnak a sarkait (csúcspontjait) A,B,C,D-vel, átlóinak metszéspontját, azaz a szoba középpontját O-val.

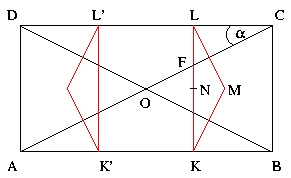OA, OB, OC, OD szakaszok felezőmerőlegesein vannak azok a pontok, melyek egyenlő távol vannak a téglalap középpontjától és valamelyik saroktól. Ezek O-t tartalmazó félsíkjában vannak azok a pontok, melyek a középponthoz vannak közelebb. Ha a fenti félsíkok közös részét tekintjük, (ezeknek is a téglalapba eső közös részét), akkor kapjuk a komplementer ponthalmazt.
Jelöljük az OC szakasz felezőpontját F-fel, OC felezőmerőlegesének metszéspontja a DC oldalon legyen L, hasonlóan OB felezőmerőlegesének AB-vel való metszéspontja legyen K. Az ábra tengelyes szimmetriája alapján KLBC KL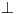AB és KLM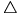 egyenlő szárú.
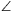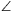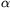Merőleges szárú szögek miatt KLM=DCA=. FCL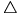 is derékszögű és van egy 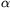hegyesszöge 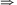FCL hasonló ACD-höz. Pitagorasz tétele alapján


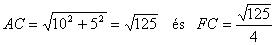
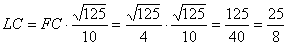
Hasonlóság miatt \(\displaystyle {LC\over FC}={AC\over DC}={\sqrt{125}\over10}\)
Legyen N az LK szakasz felezőpontja. KLM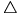 egyenlő szárú 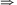MN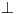KL, és KLM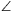= 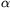; ezért az LNM háromszög hasonló az ACD háromszöghöz. Így tehát .
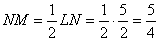A hatszöget felbonthatjuk az LKK'L' téglalapra, valamint két egybevágó háromszögre.

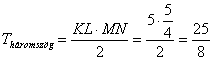
A téglalap LL' oldalát megkapjuk: .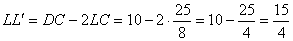

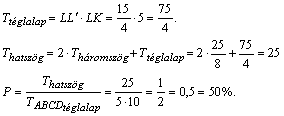
71.

Egy r sugarú kör kerületén megjelöltünk egy P pontot. Ezután, ha a körlapon találomra kiválasztunk egy pontot, mennyi annak a valószínűsége, hogy az 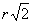-nél távolabb lesz P-től?

Megoldás:

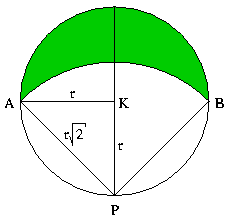P középpontú 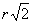sugarú körön kívül vannak azok a pontok, melyek P-től -nél távolabb vannak. A két kör metszéspontját jelöljük A-val és B-vel. A körök AB ívei által határolt holdacskán belül vannak a kívánt tulajdonságú pontok.
A keresett valószínűség kiszámításához a satírozott terület és az r sugarú kör területének arányát kell megállapítani.
AKP 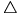derékszögű, mert oldalaira igaz a Pitagorasz tétel megfordítása: 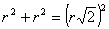Tehát 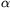=90^o , 2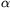=180^o, 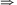A, K és B pontok egy egyenesbe esnek, ezért A és B a kör egyik átmérőjének végpontjai.
Az ábrán látható vonalkázott terület kiszámítása (a rajz jelöléseit használva) :

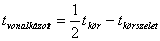
A P középpontú körhöz tartozó körszelet területét megkapjuk, ha az AB ívhez tartozó körcikk területéből kivonjuk az ABP háromszög területét. Pitagorasz tételének megfordítása szerint ABP háromszög derékszögű, mivel 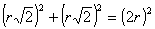, tehát .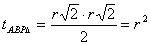
Mivel az ABP háromszög derékszögű, a körcikk területe az 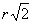sugarú kör területének negyede. .
   
   
   
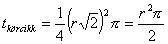
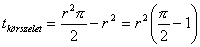
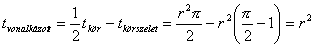
A teljes kör területe .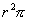
   

72.

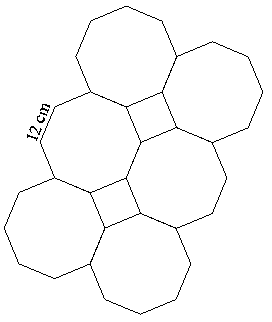Az ábrán látható mozaikparkettán hányszor nagyobb a piszokfoltok előfordulásának valószínűsége a szabályos nyolcszögben, mint a kiegészítő kis négyzetben?
Megoldás:

Szabályos nyolcszögekből és ugyanakkora oldalú négyzetekből tetszőlegesen nagy síkfelület beborítható úgy, hogy ugyanannyi nyolcszöget használunk fel, mint négyzetet. Ezért a valószínűséghez elég kiszámítanunk, hányad része a nyolcszög területe a négyzetből és nyolcszögből álló elem területének.
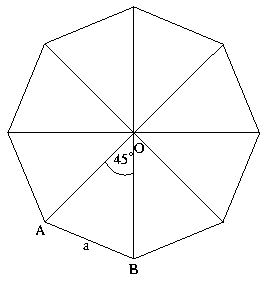
A szabályos nyolcszög felbontható nyolc egybevágó egyenlő szárú háromszögre, melynek alapja a, szárszöge pedig 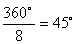. Ezeknek alaphoz tartozó magassága 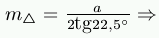területük: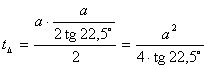
Így a nyolcszög területe: .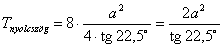
.
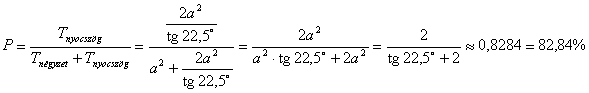Észrevehetjük, hogy az eredmény független a nyolcszög oldalától.

73.

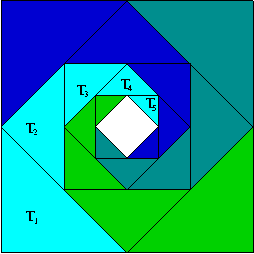Az egységoldalú négyzet oldalait megfelezve, és az osztópontokat összekötve egy újabb négyzetet kapunk.
Mi lesz a valószínűsége, hogy az ábrán véletlenszerűen kiválasztott pont a satírozott tartományba kerül, ha

1. ha az ábrán 5 négyzet van
2. a négyzetek rajzolását képzeletben vég nélkül folytatjuk?

Megoldás:

1. Az egységoldalú négyzetből levágott egyenlőszárú derékszögű háromszög területe:\(\displaystyle T_1={1\over8}\)
   Minden újabban megrajzolt háromszög területe éppen fele az előzőleg megrajzolt háromszög területének, így \(\displaystyle T_2={1\over16}\), \(\displaystyle T_3={1\over32}\), \(\displaystyle T_4={1\over64}\), \(\displaystyle T_5={1\over128}\).
   A besatírozott területet a fenti öt háromszög területének az összege adja: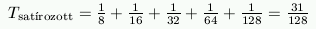
   .
   A keresett valószínűség a fenti érték és a 1 egységnyi négyzet területének a hányadosa: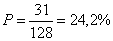
   
2. Ha belegondolunk, hogy az ábra 4 egybevágó "csigaház szerű" síkidomból épül fel, akkor világos, hogy a vég nélküli rajzoláskor a besatírozott terület: \(\displaystyle T={1\over4}\).
   Mivel a kiindulási négyzet terület: 1, ezért a keresett valószínűség: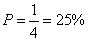
   
   Ha a végtelen mértani sorokra vonatkozó képlettel számoltunk volna: \(\displaystyle a_1={1\over8}\), \(\displaystyle q={1\over2}\), \(\displaystyle s={a\over{1-q}}\), és így \(\displaystyle s={1\over4}\).

74.

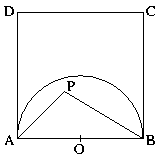
Egy 1 egység oldalú ABCD négyzet belsejében vegyünk fel véletlenszerűen egy P pontot. Mennyi a valószínűsége annak, hogy az így keletkező ABP háromszög tompaszögű lesz?

Megoldás:

Az ABP háromszögben A-nál és B-nél nem lehet tompaszög, mivel AP és BP egy derékszögű szögtartomány belsejében vannak, így a szögek ott kisebbek, mint 90^o. Így ABP háromszögben csak P-nél lehet tompaszög.
Vizsgáljuk meg, mikor látszik az AB szakasz a P pontból tompaszögben. Thalész tétele következményeként ehhez P pontnak az AB fölé írt Thalész körön belül kell lennie. A kedvező P pont tehát egy AB átmérőjű (1/2 sugarú) félkörön belül van.

75.

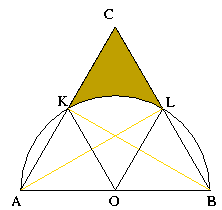
Egy 2 egység oldalú ABC szabályos háromszög belsejében vegyünk fel véletlenszerűen egy P pontot. Mennyi a valószínűsége annak, hogy az így keletkező ABP háromszög hegyesszögű lesz?

Megoldás:

Bárhogy vesszük fel P pontot, az ABP háromszögben A-nál és P-nél 60^o-nál kisebb szög keletkezik, így annak szükséges és elégséges feltétele, hogy ABP háromszög hegyesszögű legyen, az, hogy P-nél is hegyesszög legyen. Ehhez az kell, hogy P kívül legyen AB szakasz mint átmérő fölé írt Thalész körön. A feltételnek tehát a satírozott terület felel meg.
AB Thalész köre AC és BC oldalakat K illetve L pontokban metszi. Mivel ezek a pontok rajta vannak AB Thalész körén, AKB és ALB háromszögek derékszögűek. Mivel az ABC háromszög egyenlő oldalú, az AL illetve BK magasságok felezik az oldalakat. Mivel A-nál és B-nél 60^o-os szög van, ezért AOK és BOL háromszögek egyenlő oldalúak 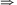OK=OL=1.
A satírozott területet megkapjuk tehát, ha az ABC háromszög területéből kivonjuk az AOK és OBL háromszög területét, valamint az O középpontú 1 egység sugarú 60^o-os körcikk területét.
Mivel az a oldalú egyenlő oldalú háromszög területe ,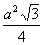

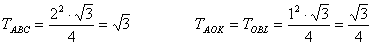
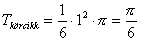
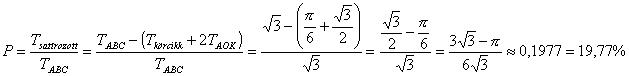
76.

Egység sugarú félkörbe 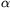^o -os derékszögű háromszöget írunk az ábrán látható módon. Mennyi a valószínűsége, hogy az ábrán véletlenszerűen kiválasztott pont a háromszögön belül van, ha 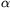=30^o?
Mekkorának válasszuk a háromszög 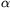szögét, hogy egy véletlenszerűen kiválasztott pont

1. a lehető legnagyobb valószínűséggel essen a háromszög belső tartományába
2. azonos valószínűséggel kerüljön a háromszög belső illetve külső tartományába ?

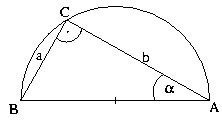Megoldás: A félkör területe:

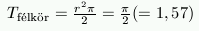
Az ABC háromszög egy szabályos háromszög fele, ezért oldalai:
    a=1                \(\displaystyle b=\sqrt3\)
A háromszög területe: \(\displaystyle T_{\triangle}={ab\over2}={\sqrt3\over2}(=0,87)\)
A keresett valószínűség:

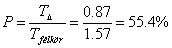
1. A háromszög oldalai:     a=2sin 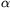               b=2cos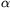
   A háromszög területe: \(\displaystyle T_{\triangle}={ab\over2}={4\sin\alpha\cos\alpha\over2}=\sin2\alpha\)
   A keresett valószínűség akkor lesz maximális, ha a háromszög területe a lehető legnagyobb.
   Ez akkor teljesül, ha sin2\(\displaystyle alpha\)=1, innen \(\displaystyle alpha\)=45^o, azaz egyenlő szárú háromszöget rajzolunk a félkörbe.
2. A két terület akkor lesz egyenlő, ha:
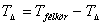   Azaz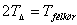
   Innen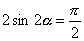
   Ebből az egyenletből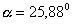

77.

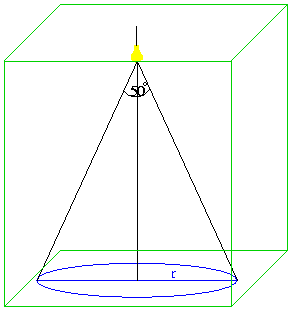
Az ábrán látható szoba mennyezetén levő lámpa legszélső fénysugara 25^o-os szöget zár be a függőlegessel. Mennyi a valószínűsége annak, hogy megtaláljuk a leejtett kontaktlencsénket ebben a rosszul kivilágított szobában? A szoba méretei: Hossza 3,8m, szélessége 3,2m, a lámpa aljának magassága 2,85m.

Megoldás:

A valószínűség kiszámításához meg kell tudnunk, hogy a szoba alapterületének mekkora része világos, azaz hogy mekkora a fénykör. A lámpa a szobának egy kúp alakú részét világítja meg. Ennek tengelymetszete egy egyenlő szárú háromszög. A háromszög alaphoz tartozó magassága 2,85m, és szárszöge 50^o.
Így: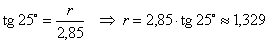

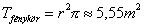
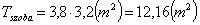
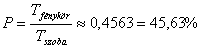
78.

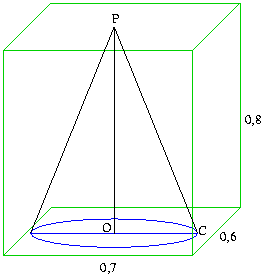Az ISS űrállomáson egy téglatest alakú tartályban elveszett egy igen fontos csavar, és most ott lebeg valahol a teljes sötétségben az űrhajós legnagyobb bánatára. Mielőtt egy mágnessel kicsalogatná, meg szeretné találni. A tartály tetején van egy kis lyuk, melyen át bevilágít a szemközti fal felé. Az űrhajós zseblámpája olyan kúp alakú fényt ad, melynek nyílásszöge 40o. Mennyi a valószínűsége annak, hogy mielőtt elfordítaná a lámpát más irányba is, az első pillanatban meglátja az igen kicsi csavart? A tartály méretei az ábrán láthatók.

Megoldás:

A szerencsés megpillantás valószínűségét megkapjuk, ha kiszámítjuk a fénykúp és a tartály térfogatának hányadosát. A tartály térfogata:
A fénykúp nyílásszöge 40^o, magassága 0,8m. Sugara a POC derékszögű háromszögből kiszámítható:
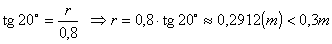, tehát a teljes kúp a téglatest belsejében van. .

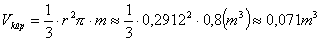
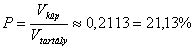
79.

Zoli edzésről este 9 és 10 óra között szokott hazajönni. Édesanyja meleg vacsorával várja. Mennyi annak a valószínűsége, hogy a frissen sütött étel nem fog 15 percnél tovább várni Zolira, de neki sem kell 15 percnél tovább várakoznia a vacsorára?

Megoldás:

A vacsora készüljön el 9 óra x percre, Zoli pedig 9 óra y perckor érkezik haza. Ideális helyzet, ha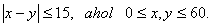
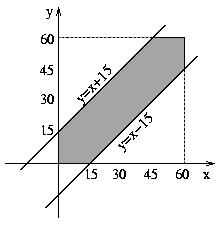
Az ilyen tulajdonságú x,y változóknak egyértelműen megfeleltethetünk egy P(x;y) pontot a koordinátasíkon (természetesen ezen pontok egy 60×60-as négyzet belső tartományának pontjai).
Pl.: P(3;16) azt jelenti, hogy a vacsora 9 óra 3 perckor lett kész, és Zoli 9 óra 16 perckor érkezett haza, azaz a vacsora csak 13 percet hűlt, tehát még ehető állapotban van.
Alakítsuk át az 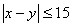egyenlőtlenséget:
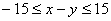. Innen 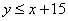az és az 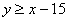összefüggéseket kapjuk. Ezeknek megfelelő pontokat a koordinátasíkon a következő ábrán vonalkázással jelöljük. A kedvező pontok egy hatszöget alkotnak, melynek területe:

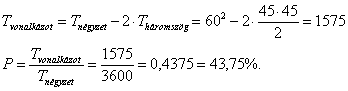
Az ideális állapot bekövetkezésének valószínűsége 44% körül van.

80.

Véletlenszerűen három részre törve egy d hosszúságú pálcát, mennyi a valószínűsége annak, hogy a kapott darabokból háromszöget lehet összerakni?

Megoldás:

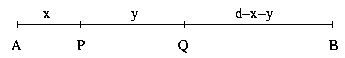
Legyen az AB=d hosszúságú pálcán a két töréspont P és Q. Így három darab keletkezik: AP=x; PQ=y és QB=d-(x+y).
Ezekből akkor lehet háromszöget készíteni, ha igaz rájuk a háromszög egyenlőtlenség, azaz bármely kettő hosszának összege nagyobb a harmadik hosszánál:

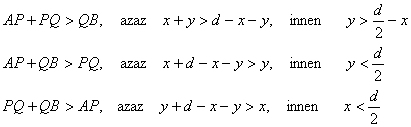
Azok a pontok, melyek mindhárom egyenlőtlenséget kielégítik, és amelyekre x,y>0 és d>x+y, a alábbi ábrán láthatóak.

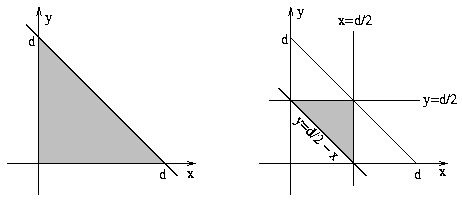
Ami a teljes eseményt illeti, a koordinátasíkon azok a P(x;y) pontok jöhetnek szóba, melyekre a kezdeti feltételek miatt 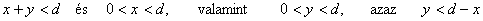, amelyek egy háromszög belső tartományának pontjai.
A két háromszög területének aránya megegyezik a keresett valószínűséggel:

  1. rész   2. rész   3 rész   4. rész   5. rész   6. rész   7. rész