Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:
VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek
1. rész
1. rész 2. rész 3. rész 4. rész 5. rész 6. rész 7. rész
Egy kis bevezetés
A világban való vizsgálódásunk során alapvetően kétféle jelenséggel találkozhatunk. Az egyik az, amikor előre meg tudjuk mondani, hogy mi fog történni. Például, ha egy alma leszakad az ágról, és nincs a környéken pad, bokor stb., akkor leesik a földre. Ezt, hogy leesik, ,,eseménynek'' nevezzük. Másik esemény például, hogy az alma nem esik le. (Ez ebben az esetben nem következik be.)
Az ilyen jelenségeket nevezzük determinisztikus jelenségnek.
A másik fajta jelenség például a lottóhúzás: nem tudjuk előre megmondani, hogy a sok esemény közül melyik fog bekövetkezni: melyik lesz az az öt szám, amit ki fognak húzni. (Persze ha pontosan tudnánk, a golyók hogyan helyezkednek el az urnában, és a forgás hatására hogy mozognak, és még sok mindent tudnánk, akkor meg tudnánk mondani, hogy mik lesznek a kihúzott számok.)
A lényeg az, hogy ha nem ismerjük eléggé a körülményeket, a feltételeket, akkor nem tudjuk előre megmondani, mi fog történni. Az ilyen jelenségeket hívjuk véletlen jelenségeknek.
Vannak olyan jelenségek, amiket sokszor meg tudunk figyelni. Ilyen például a lottóhúzás. Egy ilyen megfigyelést szoktak ,,kísérletnek'' is nevezni.
Egy kísérlet kimenetelére különböző állításokat fogalmazhatunk meg. Ha az állítás igaz vagy hamis volta csak a kísérlet kimenetelétől függ, akkor az állítást eseménynek nevezzük. Jelölése általában nagybetűvel történik. Ilyen például - a lottóhúzásra vonatkozó - ,,A kihúzott számok között van páratlan.'' Legyen ez az A esemény. Egy másik állítás : ,,A kihúzott számok között szerepel a 2.'' Legyen ez a B esemény. Egy harnmadik állítás: ,,A kihúzott számok között pontosan egy páratlan van.'' Legyen ez a C esemény. Egy negyedik állítás: ,,A kihúzott számok között pontosan két páratlan van.'' Legyen ez a D esemény. Egy ötödik állítás: ,,A kihúzott számok között pontosan három páratlan van.'' Legyen ez a E esemény. Egy hatodik állítás: ,,A kihúzott számok között pontosan négy páratlan van.'' Legyen ez a F esemény. Egy hetedik állítás: ,,A kihúzott számok között pontosan öt páratlan van.'' Legyen ez a G esemény. Egy nyolcadik állítás: ,,A kihúzott számok között van páratlan vagy van páros.'' Legyen ez a H esemény. Egy kilencedik állítás: ,,A kihúzott számok között se páratlan, se páros nem szerepel.'' Legyen ez a I esemény. Egy tizedik állítás: : ,,A kihúzott számok között nem szerepel a 2.'' Legyen ez a J esemény.
Események összegén azt az eseményt értjük, ami pontosan akkor következik be, ha az események közül legalább az egyik bekövetkezik. Jelölése: +. Pl. A=C+D+E+F+G. Két esemény szorzata az az esemény, mely pontosan akkor következik be, ha mindkét esemént bekövetkezik. Pl. B.E=,,Pontosan két páros szám van, melyek közül az egyik a 2.'' Egy A esemény kiegészítő eseménye az az esemény, mely pontosan akkor következik be, ha A nem. jelölése: \(\displaystyle \overline{A}\). Pl.: \(\displaystyle \overline{B}=J\) és nyilván \(\displaystyle \overline{J}=B\). Az az esemény, ami soha nem következik be, a lehetetlen esemény. Jel.: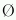 
. Pl. G=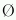. Két esemény kizárja egymást, ha szorzatuk 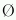, pl. EF=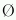. Az az esemény, ami biztosan bekövetkezik, a biztos esemény. Pl. B+I biztos esemény, és ált., \(\displaystyle X+\overline{X}\) biztos esemény.
Ha egy esemény előáll legalább két másik esemény összegeként, akkor összetett eseménynek nevezzük. Ha nem, akkor elemi eseménynek.
Sokszor találkozunk olyan kísérletekkel, amelyekben az elemi események száma véges és esélyük (valószínűségük) megegyezik - ekkor klasszikus valószínűségi problámáról beszélünk. Ekkor, ha B egy tetszőleges esemény:
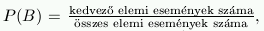ahol kedvező elemi esemény az, ami esetén a B esemény bekövetkezik (végül is az összes olyan elemi esemény, amit B ,,tartalmaz''); P(B) pedig B valószínűségét jelöli. Általában:
Egy konkrét kísérlet összes lehetséges eseményeihez tartozik egy-egy számérték, amit az illető esemény valószínűségének nevezünk, és amelyre a következő axiómák teljesülnek:
I. axióma: Minden A eseményre 0\(\displaystyle le\)P(A)\(\displaystyle le\)1
II. axióma: P(biztos esemény)=1, P(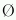)=0
III. axióma: Ha AB=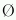, akkor P(A+B)=P(A)+P(B)
Például: Egy érmét kétszer feldobva:
|
P(írások száma=1)=1/3.
De itt valójában nem erről van szó, hiszen az első oszlop 2 elemi eseményt takar. A táblázat helyesen:
|
P(írások száma 1)=2/4=1/2.
Láthatjuk, hogy fiigyelni kell, mikor az eseményeket lebontjuk elemi eseményekre; és azt is meg kell nézni, hogy egyenlő esélyűek-e, azaz, hogy számolhatunk-e a klasszikus valószínűségi problémára vonatkozó képlettel.
Ha egy kísérletet n-szer elvégzünk, és egy bizonyos esemény ennek során k-szor következik be, akkor a k számot az esemény gyakoriságának, a k/n számot pedig a relatív gyakoriságának nevezzük.
Megfigyelhetjük, hogy ha egy eseményre vonatkozóan egy kísérletet sokszor elvégzünk, akkor a relatív gyakoriság (egy idő után) az esemény valószínűsége körül fog ingadozni.
Néhány kombinatorikai alapfogalom
1. kérdés: n különböző elemet hányféleképpen tudunk sorba rakni?
Válasz: Az 1. helyre bármelyiket tehetem az n elem közül, a 2. helyre már csak a maradék n-1 elem közül tehetem valamelyiket, és így tovább. Tehát a válasz: n(n-1)(n-2).3.2.1. Ezt a számot így is szokták jelölni: n! (ejtsd: n faktoriális).
2. kérdés: n különböző elemből hányféleképpen tudunk k-t kiválasztani, ha számít, hogy milyen sorrendben választjuk ki őket?
Válasz: Hasonlóan gondolkozunk, mint az előbb. A különbség csak annyi, hogy itt nem n, hanem k számot szorzunk össze: \(\displaystyle n(n-1)(n-2)\cdot(n-k+1)={n!\over (n-k!)}\).
3. kérdés: n különböző elemből hányféleképpen tudunk k-t kiválasztani, ha mindegy, hogy milyen sorrendben választjuk ki őket?
Válasz: Vessük össze az előző problémával. Csak abban különböznek, hogy itt nem számít, hogy a k elem milyen sorrendben követi egymást. (Ilyen például a lottóhúzás). Tehát ami itt 1 eset, az az előbb k! eset volt (ennyiféleképp tudnám a k elemet sorba rakni). Tehát a keresett szám: \(\displaystyle {n(n-1)(n-2)\cdot(n-k+1)\over k!}={n!\over(n-k)!k!}\). Ennek is van saját jelölése: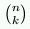 
, ejtsd: n alatt a k.
Megjegyzés: látható, hogy 