Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:
VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek
3. rész
1. rész 2. rész 3. rész 4. rész 5. rész 6. rész 7. rész
16. Leteszünk egymás mellé az asztalra 3-3 kártyát számmal lefelé: pikk hármast, pikk négyest, pikk ötöst, valamint treff hármast, treff négyest és treff ötöst. Húzunk a pikkek közül is egy lapot és a treffek közül is egy lapot. Mekkora a valószínűsége annak, hogy
- a kihúzott számok összege 8;
- a két kihúzott szám egyforma;
- a pikkek közül húzott szám kisebb, mint a treffek közül húzott;
- két különböző prímszámot húzunk?
Megoldás:
Összesen 3×3=9 pár húzható ki úgy, hogy az egyik pikk legyen, a másik treff.
- A kihúzott számok összege 8 a következő esetekben lehet:
 3 +
3 +  5 vagy
5 vagy
 4 +
4 +  4 vagy
4 vagy
 5 +
5 +  3 , azaz három a kilencből,
valószínűsége
3 , azaz három a kilencből,
valószínűsége 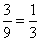 .
.
- A két kihúzott szám egyforma, ha két hármast, két négyest, vagy két ötöst húzunk. Ez három eset a kilencből,
valószínűsége
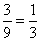 .
.
- A pikk kisebb, mint a treff:
 3 és
3 és
 4,
4,  3 és
3 és
 5,
5,  4 és
4 és
 5. Ez három eset a kilencből, valószínűsége
5. Ez három eset a kilencből, valószínűsége
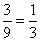 .
.
- Két különböző prímszámot választunk:
 3 és
3 és
 5 vagy
5 vagy  5 és
5 és
 3. Ez kettő eset a kilencből, valószínűsége
3. Ez kettő eset a kilencből, valószínűsége 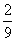 .
.
17. Leteszünk egymás mellé az asztalra 3-3 kártyát számmal lefelé: pikk hármast, pikk négyest, pikk ötöst, valamint
treff hármast, treff négyest és treff ötöst. Húzunk két kártyát közülük. Mely események valószínűsége lehet
a. 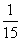 b.
b. 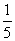 c. 40% d. 0,6
e.
c. 40% d. 0,6
e. 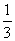
Megoldás:
Hat különböző kártyából két darabot 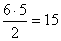 módon tudunk húzni.
Ezek a lehetőségek:
módon tudunk húzni.
Ezek a lehetőségek:
 3 3 4 4 |
 3 3 5 5 |
 3 3 3 3 |
 3 3 4 4 |
 3 3 5 5 |
 4 4 5 5 |
 4 4 3 3 |
 4 4 4 4 |
 4 4 5 5 |
 5 5 3 3 |
 5 5 4 4 |
 5 5 5 5 |
 3 3 4 4 |
 3 3 5 5 |
 4 4 5 5 |
- Olyan eseményt keresünk, aminek valószínűsége
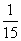 , azaz egyetlen
esetben fordul elő a tizenötből. Ilyen esemény például, hogy két négyest húzunk.
, azaz egyetlen
esetben fordul elő a tizenötből. Ilyen esemény például, hogy két négyest húzunk.
- Olyan eseményt keresünk, aminek valószínűsége
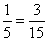 , azaz három esetben
fordul elő a tizenötből. Ilyen esemény például, hogy a két kihúzott kártyán ugyanolyan szám legyen.
, azaz három esetben
fordul elő a tizenötből. Ilyen esemény például, hogy a két kihúzott kártyán ugyanolyan szám legyen.
- Olyan eseményt keresünk, aminek valószínűsége 40%, vagyis
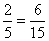 , azaz hat
esetben fordul elő a tizenötből. Ilyen esemény például, hogy a két kihúzott kártyán ugyanolyan szín (pikk vagy treff)
szerepeljen.
, azaz hat
esetben fordul elő a tizenötből. Ilyen esemény például, hogy a két kihúzott kártyán ugyanolyan szín (pikk vagy treff)
szerepeljen.
- Olyan eseményt keresünk, aminek valószínűsége
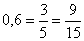 , azaz kilenc esetben
fordul elő a tizenötből. Ilyen esemény például, hogy a két kihúzott kártyán különböző szín (pikk vagy treff) szerepeljen.
, azaz kilenc esetben
fordul elő a tizenötből. Ilyen esemény például, hogy a két kihúzott kártyán különböző szín (pikk vagy treff) szerepeljen.
- Olyan eseményt keresünk, aminek valószínűsége
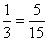 , azaz öt esetben
fordul elő a tizenötből. Ilyen esemény például, hogy a kihúzott kártyákon szereplő számok összege nagyobb legyen
nyolcnál.
, azaz öt esetben
fordul elő a tizenötből. Ilyen esemény például, hogy a kihúzott kártyákon szereplő számok összege nagyobb legyen
nyolcnál.
18. 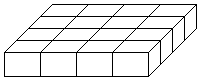 Egy téglalap alakú tepsiben sütött nagymama sütit, és amikor tálcára tette, a tetejét és az oldalát bevonta
csokikrémmel. Tálaláskor hat vágással (ahogyan a rajz mutatja) tizenhat szeletre vágta. Kiválasztunk belőle találomra
egy kockát. Mekkora a valószínűsége annak, hogy
Egy téglalap alakú tepsiben sütött nagymama sütit, és amikor tálcára tette, a tetejét és az oldalát bevonta
csokikrémmel. Tálaláskor hat vágással (ahogyan a rajz mutatja) tizenhat szeletre vágta. Kiválasztunk belőle találomra
egy kockát. Mekkora a valószínűsége annak, hogy
- csak egy oldala lesz csokis;
- ugyanannyi oldala lesz csokis, mint amennyi nem;
- feleannyi csokis oldala lesz, mint amennyi nem;
- több csokis oldala lesz, mint nem?
Megoldás:
Az egész süti négy sarkának három-három oldala csokis (három-három pedig nem), a szélén lévő sarkok közötti nyolc szeletnek két-két oldala csokis (négy-négy pedig nem), a középen lévő négy szeletnek egy-egy oldala csokis (öt-öt pedig nem), több szelet nincs.
- P(csak egy oldala lesz csokis)=
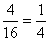
- P(ugyanannyi oldala lesz csokis, mint amennyi nem)=
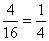
- P(feleannyi csokis oldala lesz, mint amennyi nem)=
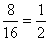
- P(több csokis oldala lesz, mint nem)= 0
19. Két dobozban számkártyákat helyeztünk el. Az egyikben 3 db-ot, ezekre 1-től 3-ig, a másikban 4 db-ot, ezekre 4-tól 7-ig írtuk az egész számokat. Mindkét dobozból egy-egy kártyát húzunk és belőlük a húzás sorrendjében egy kétjegyű számot készítünk. Állapítsuk meg a következő események valószínűségét!
- a szám nem osztható 3-mal
- a számjegyek szorzata prímszám
- a szám jegyei relatív prímek
Oldjuk meg a feladatot abban az esetben is, ha az első dobozba a 0 számkártyát is betesszük!
Megoldás:
Ha az első dobozból húzott számkártyákhoz párosítjuk a második dobozból húzottakat, akkor 3 × 4= 12 db kétjegyű
számot kapunk. Ha a másodikból húzottakhoz párosítjuk az első dobozbeli számokat, akkor 4 × 3 = 12 db számot
kapunk. Ez összesen 24 db különböző szám.
- Hárommal osztható számok: 15,51,24,42,27,72,36,63.
Hárommal nem osztható 24 - 8 = 16 db szám.
P(hárommal nem osztható) =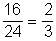 .
.
- A számjegyek szorzata prímszám: 15,51,17,71 számok esetén
P(számjegyek szorzata prímszám )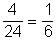 .
.
- A szám jegyei relatív prímek:
14,41,15,51,16,61,17,71,25,52,27,72,34,43,35,53,37,73 számok esetén.
P(szám jegyei relatív prímek) =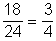 .
.
Ha az első dobozba a 0 számkártyát is betesszük, akkor az előbb számolt 24 db-on kívül még négy új szám készíthető a 40, az 50, a 60 és a 70, így összesen 28 db számunk lesz. A fenti megoldások a következőképpen módosulnak:
- A négy szám közül csak a 60 osztható 3-mal, ezért a 3-mal nem nem osztható számok száma : 28 - 9 = 19
P(hárommal nem osztható ) =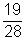
- P(számjegyek szorzata prímszám ) =
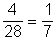
- P(szám jegyei relatív prímek) =
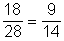
20. Mekkora annak a valószínűsége, hogy egy kétjegyű szám négyzetének utolsó számjegye 6 legyen?
Megoldás:
Összesen 90 darab kétjegyű szám van. Ezek közül azoknak végződik a négyzete 6-ra, amelyeknek utolsó számjegye 4
vagy 6. Ilyenek a 14, 16, 24, 26, ..., 94, 96, vagyis minden tízes csoportban van két megfelelő szám, összesen 2 × 9 = 18
darab. A keresett valószínűség: 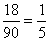 .
.
21.  Orsiék szombaton kirándulni mennek öten. Mindenkinek két-két szendvics került a közös hátizsákba, összesen négy szalámis és hat májkrémes, egyforma csomagolásban. Mekkora a valószínűsége annak, hogy Orsi két májkrémeset vesz ki magának, ha véletlenszerűen választ?
Orsiék szombaton kirándulni mennek öten. Mindenkinek két-két szendvics került a közös hátizsákba, összesen négy szalámis és hat májkrémes, egyforma csomagolásban. Mekkora a valószínűsége annak, hogy Orsi két májkrémeset vesz ki magának, ha véletlenszerűen választ?
Megoldás:
10 szendvicsből kell kettőt kivennie, ezt 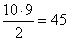 lehetséges módon teheti.
lehetséges módon teheti.
A két májkrémeset csak hat közül választhatja, mégpedig 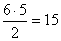 lehetséges módon.
lehetséges módon.
nnak a valószínűsége, hogy két májkrémeset vesz ki magának: 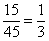 .
.
22. Az osztályba 16 lány és 14 fiú jár. Kedden két egymást követő órán sorsolni fognak egy-egy felelőt. Mekkora a valószínűsége annak, hogy
- mindkét órán lány;
- az első órán lány, a másodikon fiú fog felelni?
Megoldás:
A két órán a sorsolások egymástól függetlenek, mindkét esetben 30 gyerek közül kerül ki a felelő.
Annak a valószínűsége, hogy egy alkalommal lányt sorsolnak ki 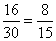 ,
annak, hogy fiút
,
annak, hogy fiút 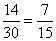 .
.
- Annak a valószínűsége, hogy mindkét órán lányt sorsolnak ki:
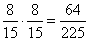 .
.
- Annak a valószínűsége, hogy az első órán lányt, a másodikon fiút sorsolnak ki:
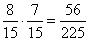 .
.
23. Egy autóban három darab kétállású (A vagy B) kapcsolóval meg lehet akadályozni az indítást: csak akkor lehet az autót elindítani, ha mindegyik kapcsoló azonos állásban van. A kapcsolókat tetszőleges helyzetben hagyva mekkora a valószínűsége annak, hogy egy ismeretlen el tudja indítani az autót?
Megoldás:
Mindegyik kapcsolónak két állása van, és ezek egymástól függetlenül működnek. Így a három kapcsoló 23=8 különböző
helyzetben lehet.
Elindítani az autót akkor lehet, ha mindegyik kapcsoló A állásban, vagy mindegyik kapcsoló B állásban van. Ez két
eset a nyolcból, tehát a valószínűsége 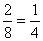 .
.
24. Kovács apuka, három gyermeke: Jani, Elek és Panni közül valamelyik kettőt szeretné elküldeni bevásárolni. Mivel a gyerekek vonakodnak, ezért apuka mind a három nevet felírja egy cédulára, és kihúz közülük két nevet. Mekkora a valószínűsége annak, hogy
- két fiú megy,
- egy fiú és egy lány,
- Panni és Elek megy vásárolni?
Határozzuk meg azt is, hogy egy-egy gyerek nevét mekkora eséllyel húzhatjuk ki!
Megoldás:
A három gyermekből kiválasztható párosok: J,E; J,P; E,P. Ez összesen három elemi esemény.
Az a. szerint számunkra csak az J,E kedvező, így a valószínűség:
P(két fiú)= 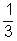
A b. szerint kedvező esemény: J,P; és E,P, ez két eset, így a valószínűség
P(egy lány és egy fiú)= 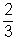
A c. szerint kedvező esemény a P,E , így a valószínűség:
P(Panni és Elek)= 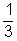 .
.
Az összes eset három különböző párosában egy-egy gyerek kettőben biztosan szerepel. Jani például a fenti
felsorolásban az első kettőben, ezért annak a valószínűsége, hogy neki mennie kell 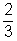 .
Ugyanez az arány igaz bármelyik gyerekre.
.
Ugyanez az arány igaz bármelyik gyerekre.
25. Ezen a héten Zsolt és Dani a hetesek az osztályban. Minden nap pénzfeldobással döntik el, hogy melyikük törli le a táblát az órák előtt: ha a fej van felül, akkor Zsolt, ha az írás van felül, akkor Dani.
- Mekkora a valószínűsége annak, hogy mind az öt nap Zsolt törli a táblát?
- Mekkora a valószínűsége annak, hogy Zsolt egy nap, Dani négy nap törli a táblát?
Megoldás:
Mind az öt nap kétféle eredménye lehet a pénzfeldobásnak: írás vagy fej, ezért az egész héten összesen 25=32 különböző táblatörlési rend lehetne.
- Ha mind az öt nap Zsolt törli a táblát, akkor a 32-ből csak egy eset lehetséges: minden nap fejet dobtak. Ennek a
valószínűsége:
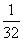 .
.
- Ha Zsolt egy nap, Dani négy nap törli a táblát, akkor öt eset lehetséges: az öt nap közül az egyiken dobtak fejet.
Ennek a valószínűsége:
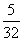 .
.
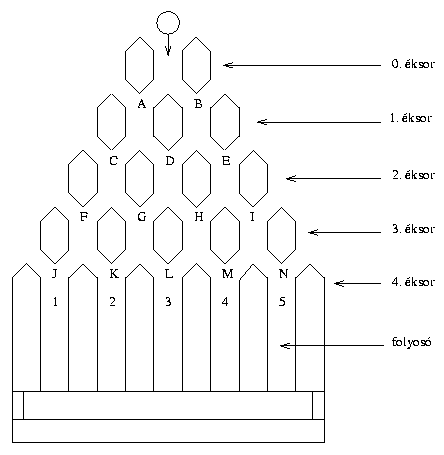
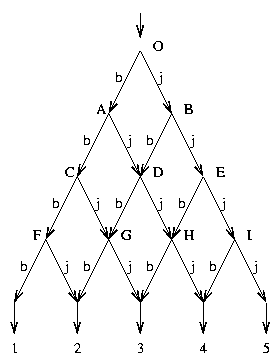
26. Az ábrán látható a Galton deszka rajza és az abba bedobott golyó lehetséges útvonalai. A golyót bármelyik nyíláson is dobjuk be, azt a fából készült ékek az elágazásoknál egyenlő valószínűséggel terelik két irányba.
 |
 |
Indítsuk a golyókat a felső nyíláson át!
- Számítsuk ki, hogy az egyes elágazási pontokhoz mekkora valószínűséggel juthat el a golyó!
- Határozzuk meg mind az 1,a 2, a 3, a 4 és az 5 folyosókba való megérkezés valószínűségét!
Megoldás:
- Az eszköz tengelyes szimmetriája miatt megállapíthatjuk, hogy
P(A)=P(B), P(C)=P(E), P(F)=P(I), P(G)=P(H). 
Az O pontból indulva az első "döntés" valószínűsége
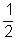 .
Ez minden elágazásnál, az előző "döntéstől" függetlenül újra megismétlődik. Ilyenkor az egyes útszakaszok választásának
valószínűségét összeszorozzuk.
.
Ez minden elágazásnál, az előző "döntéstől" függetlenül újra megismétlődik. Ilyenkor az egyes útszakaszok választásának
valószínűségét összeszorozzuk.
Például a C, vagy az E pontba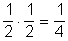 valószínűséggel érkezik a golyó, mert
A-ba, illetve B-be is
valószínűséggel érkezik a golyó, mert
A-ba, illetve B-be is 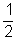 , onnan tovább C-be, illetve E-be is
, onnan tovább C-be, illetve E-be is 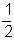 valószínűséggel
gurul tovább.
valószínűséggel
gurul tovább.
Akkor viszont, amikor például a golyó a D pontba érkezik, a válaszható utak valószínűsége összeadódik, mivel ide a golyó vagy b,j, vagy j,b, útvonalon érkezhet, tehát A D pontba érkezés valószínűsége:
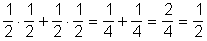
Megállapíthatjuk, hogy az egy sorban lévő elágazásokba nem egyenlő valószínűséggel kerülnek a golyók, és egy-egy sorban a megérkezések valószínűségének összege mindig 1.
Például: P(C )+P(D) +P(E) =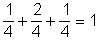
Így a keresett valószínűségek:START A 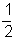
B 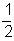
C 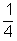
D 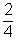
E 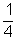
F 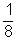
G 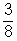
H 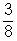
I 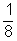
- Az előző gondolatmenetet folytatva: P(1) = 1/2 × P(F) = 1/16; P(2) = 1/2 × P(F) + 1/2 × P(G) = 1/4; P(3) = 1/2 × P(G) + 1/2 × P(H) = 3/8; P(4) = P(2) = 1/4; P(5) = P(1) = 1/16.
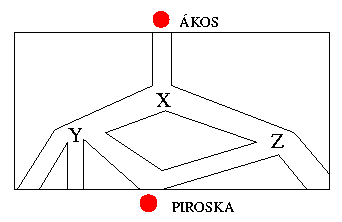
27. Ákos, akit a város parkjának egyik sétánya végén várja a barátnője a rajzon látható útvonalak bármelyikét választva juthat el oda. Mekkora valószínűséggel találkozhat barátnőjével?
Megoldás:
Ákos az X elágazásnál 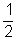 valószínűséggel, az Y elágazásnál
valószínűséggel, az Y elágazásnál
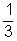 valószínűséggel, a Z elágazásnál ismét
valószínűséggel, a Z elágazásnál ismét 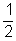 valószínűséggel dönt. Ahhoz a kijárathoz, ahol a barátnője áll, vagy Y, vagy Z pontból érkezhet.
Így annak a valószínűsége, hogy találkozik a barátnőjével:
valószínűséggel dönt. Ahhoz a kijárathoz, ahol a barátnője áll, vagy Y, vagy Z pontból érkezhet.
Így annak a valószínűsége, hogy találkozik a barátnőjével:
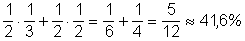
28. Az első három definíciót zöld színű cédulára, a negyediket és az ötödiket kék színű cédulára írtuk. Mind az öt definíció valamilyen paralelogramma tulajdonságot fogalmaz meg. A cédulákból úgy húzunk ki kettőt, hogy az egyik zöld színű, a másik kék színű legyen. Mekkora annak a valószínűsége, hogy mindkét cédulán egy általános paralelogramma tulajdonságát olvashatjuk?
| A "zöld" definíciók: I. Átlói merőlegesek egymásra II. Szemközti szögei egyenlők III. Átlói felezik a szögeket |
A "kék" definíciók: IV. Szögeinek összege 360o V. Átlói felezik egymást. |
Megoldás:
Ha a "zöld" definíciókból választunk és azokhoz párosítjuk egyenként a "kékeket", akkor 3 × 2 = 6 féle pár
készíthető, ha fordított sorrendben választunk, akkor is ugyanezek a párok jönnek létre, ezért összesen 6
különböző pár készíthető a kétféle színű cédulára írt öt definícióból.
Ezek közül általános paralelogramma tulajdonság a II - IV és a II - V párokon olvasható.
Tehát P(mindkét cédulán általános paralelogramma tulajdonság van)= 2/6=1/3.
29. Kartonpapírból kivágunk három különböző háromszöget. Válasszunk ki találomra ezek közül két háromszöget! Mekkora a valószínűsége annak, hogy a kiválasztottakból egy négyszöget tudunk kirakni úgy, hogy azokat egy-egy oldaluknál összeillesztjük?
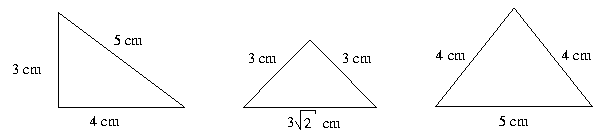
I - II, I - III, II - III.
A párokból akkor tudunk négyszöget kirakni, ha a két háromszögnek legalább egy-egy ugyanakkora oldala van.
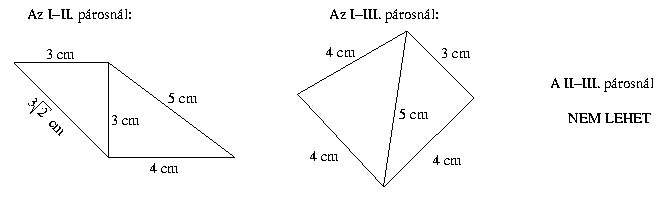
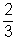 .
.
30. Egy 2 cm, egy 3 cm, egy 5 cm és egy 6 cm hosszúságú szakaszból találomra kiválasztunk hármat. Mekkora a valószínűsége annak, hogy azokból háromszöget tudunk szerkeszteni?
Megoldás:
Összesen négy különböző számhármast választhatunk, mert a négy szakasz közül egyet mindig ki kell hagyni, és ezt négyféleképpen tehetjük meg. A kiválasztott szakaszokból akkor lehet háromszöget szerkeszteni, ha azok hossza:
| 3 cm, | 5 cm, | 6cm, | mert 3 + 5 > 6 | |
| vagy | 2 cm, | 5cm, | 6cm, | mert 2 + 5 > 6 |
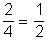 .
.

